LENGTH CONTRACTION... any
two occupied points in space are furthest apart in their rest
frame.

L = L0[1 -
(v/c)2]1/2

q at rest. |

q moving to right.
|

Contraction occurs along the
line of relative motion, only.


The magnetic field can be
thought of as a relativistic correction to the usual electric
field. Effects due to a magnetic field in one frame of reference
can be due entirely to an electric field in another.
Imagine a neutral "wire" which is a hollow tube with protons
moving in one direction along it, and electrons moving in the
opposite direction. Both (equal) currents produce a
magnetic field in the same direction, which interacts with a
moving charge outside the wire. Now ride along with the
moving charge. Since it has velocity zero, the magnetic
field cannot exert a force on it, but the wire is NOW CHARGED
and the resulting electric field of the wire exerts a force on
the charge! In a relativistic formulation of physics,
electric and magnetic fields are interchangeable.
 |
 |
If you look at the algebraic form
of the (Lorentz)
transformations of space and time coordinates from one
inertial frame to another, they are quite different. In other
words, a space coordinate like the position vector r
transforms very differently compared to the scalar time
coordinate t. A relativistic expression for momentum
results from realizing that p needs to transform like r,
so we need to define p = m(dr/dτ), where τ is the
proper time. A relativistic expression for kinetic energy
results from realizing that energy should transform like time t,
so that E = mc2(dt/dτ). Then use the
relation between dt and dτ to get the final result.
E = KE + mc2
and E2 = (pc)2 + (mc2)2
for a free particle!
A very useful equation! v/c
= (pc)/E.
Note that if a particle has
mass, it takes an infinite amount of force and an infinite
amount of work to make v → c. Thus, no particle with
mass can ever travel at c. But if a particle has NO
mass, it can never travel at any speed OTHER THAN c, no
matter how much momentum or kinetic energy it has! It's
vital to realize that intrinsic properties of particles
are the same in all inertial frames of reference: charge, mass,
magnetic moment, etc.
 '
'
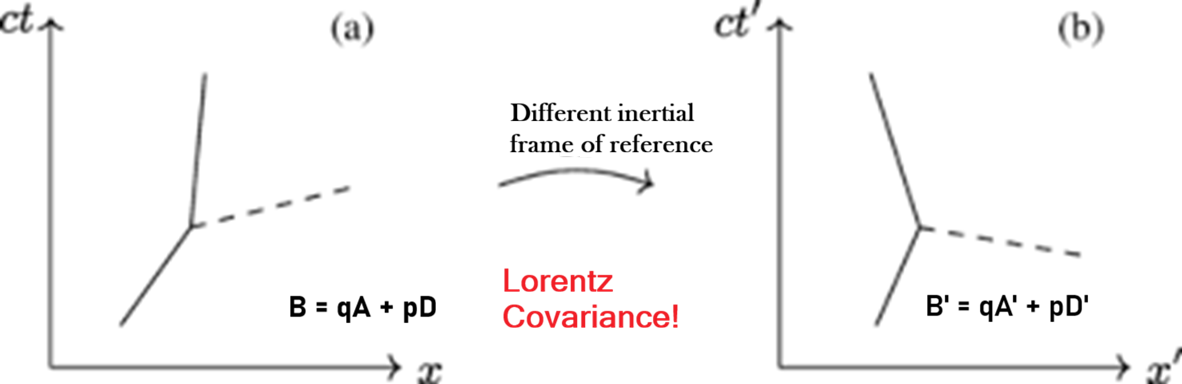
Physical laws written in a Lorentz
covariant (four-vector) form have the same mathematical form in
any and all inertial frames of reference.
WHAT
IS A FOUR VECTOR?
HOW FAR CAN WE SEE?
NEXT
Back
 '
'