 |
 |
 |
| |
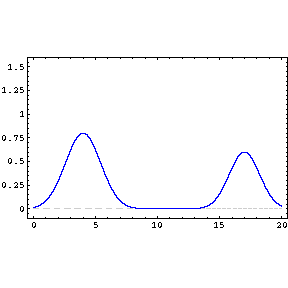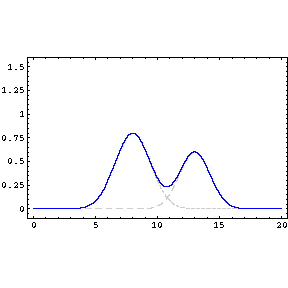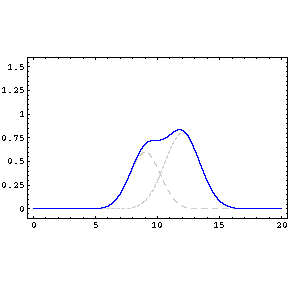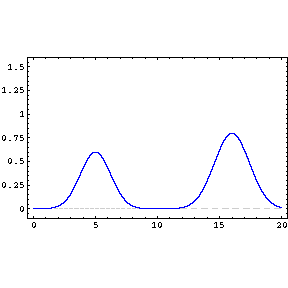
Two or more different waves in the same medium combine algebraically: y(x,t) = y1(x,t) + y2(x,t) + …
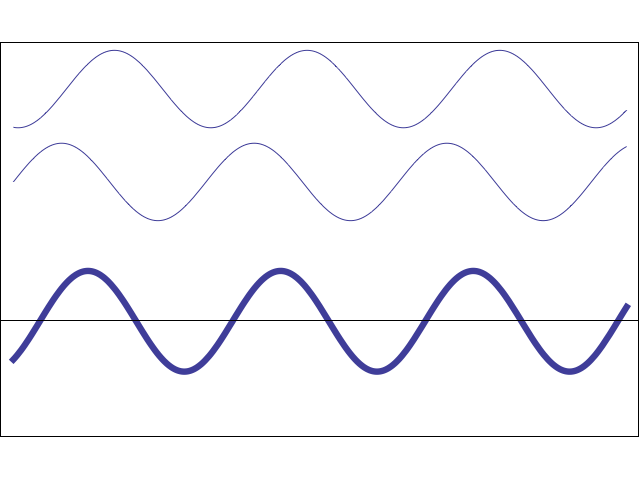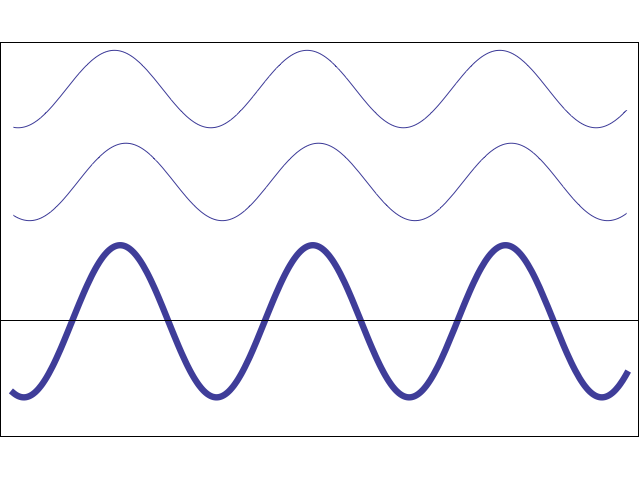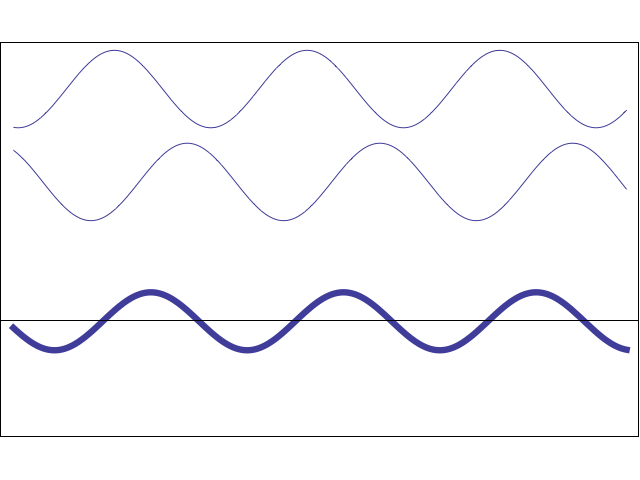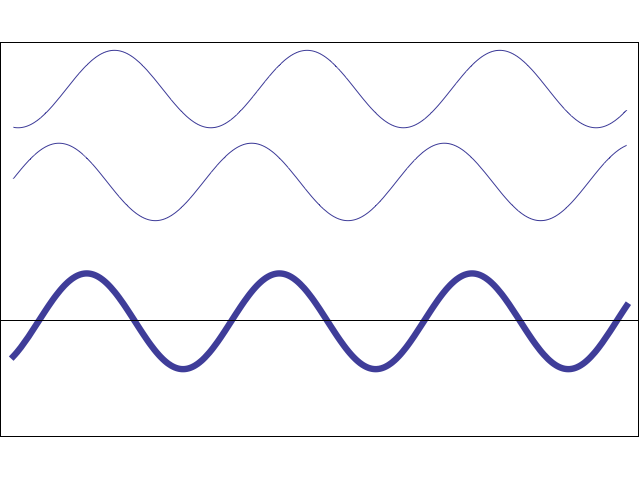
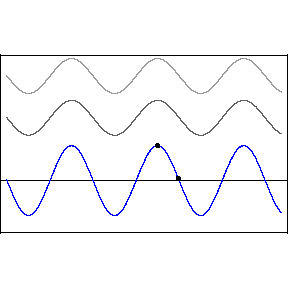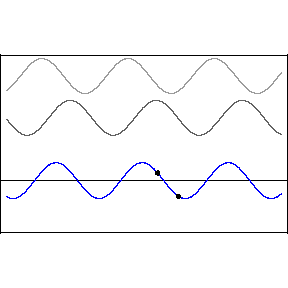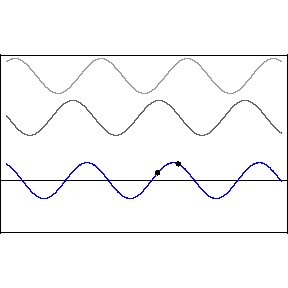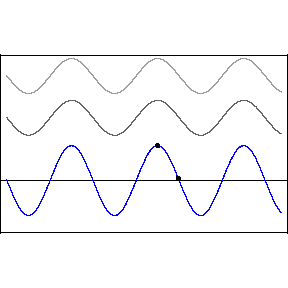
Two waves moving in the same direction with the same amplitude but different phase speeds, vp.
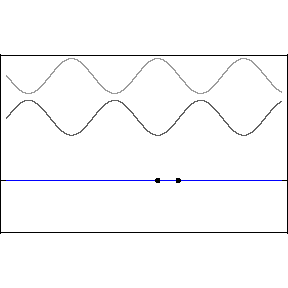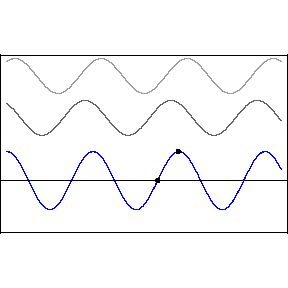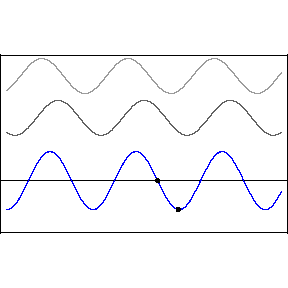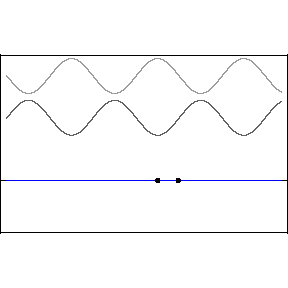
Two waves of the same amplitude and frequency moving in opposite directions with the same phase speed produce the phenomenon known as a “standing wave.”
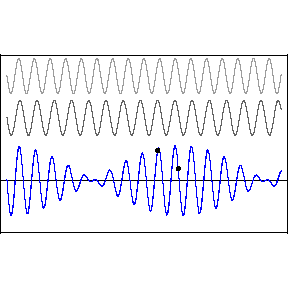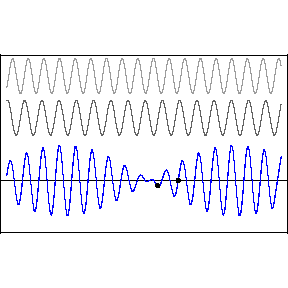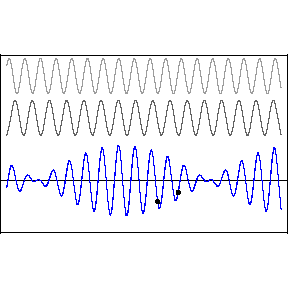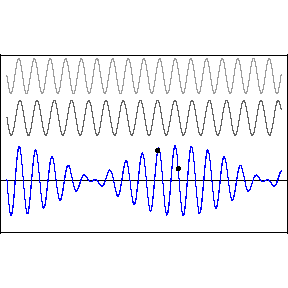
Two waves with the same amplitude and speed but slightly different frequencies produce the amazing and beautiful phenomenon of “beats.”

| |