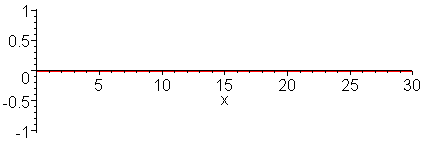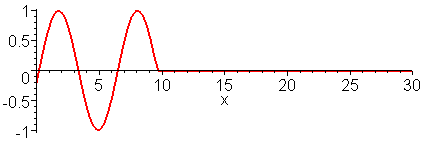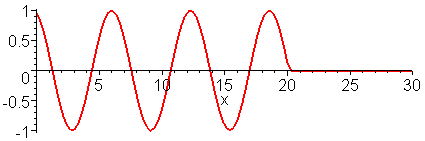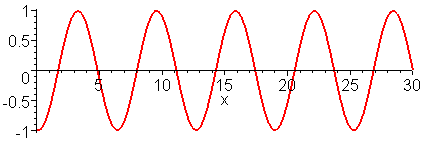WAVES!
• Transverse Waves!

• Longitudinal Waves!

Consider transverse waves to
begin with. For a wave moving to the right, the wave function is
of the general form:
y(x,t) = A cos[kx
- ωt].
A good wave applet!
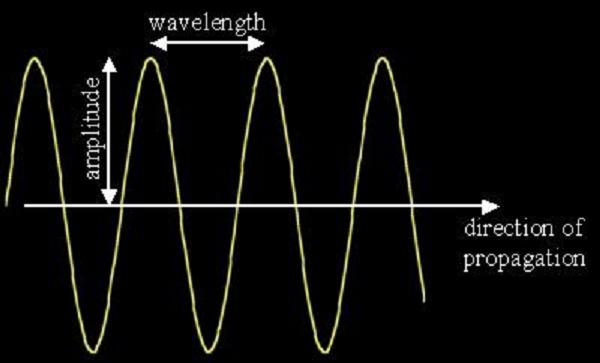
In terms of the wave parameters, A,
k and ω, the amplitude of the wave is A,
the wavelength of the wave is λ = 2π/k and the frequency
is f = ω/2π while the wave period is 2π/ω. The
phase speed of the wave is vp = ω/k.
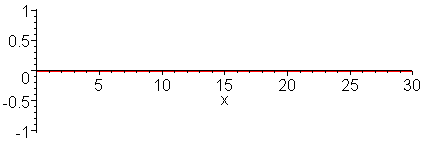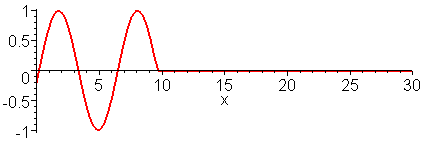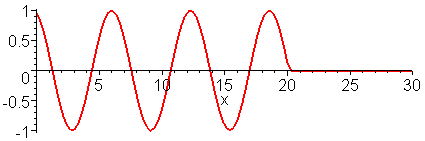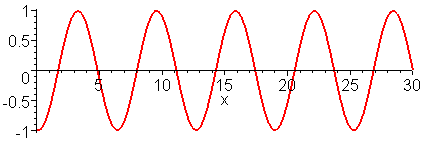
Note that the wave function can be
written as:
y(x,t) = A cos[k(x
- vpt)].
Thus, a wave moving to the left is
written as:
y(x,t) = A cos[k(x
+ vpt)] = A cos[kx + ωt].
How to derive the wave
equation from Newton's 2nd Law, applied to a vibrating string.

Reflection!
SOUND!
Types of Waves!
Back