• Any unsupported object whatsoever, near the earth's surface, accelerates toward the center of the earth at a constant rate of about 10 meters per second per second. We define a vector g which points at the earth's center and has a magnitude of g = 10 m/s2.
• An object which is released from rest moves toward the earth with an increasing v(t) = gt, and its distance moved downward increases according to d(t) = (1/2)gt2.
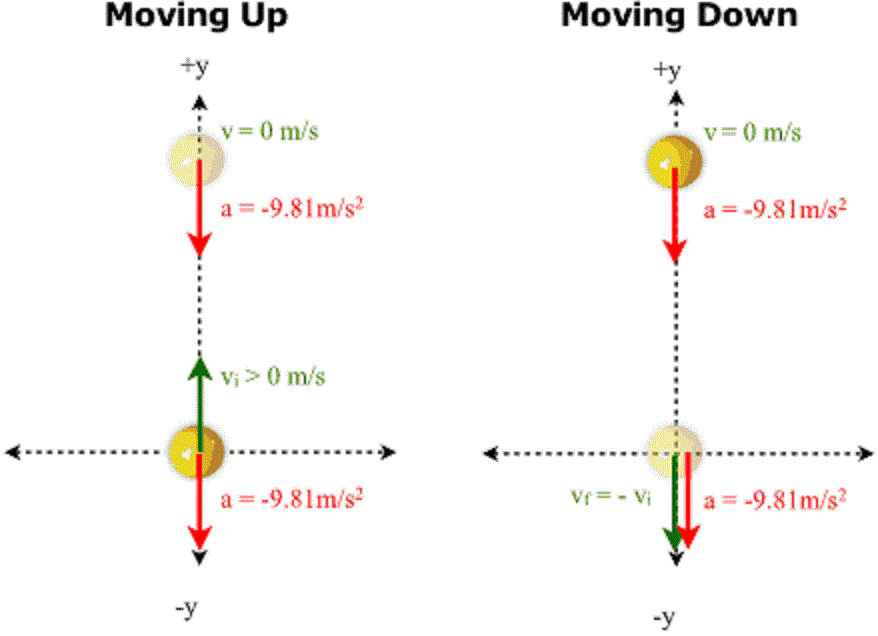
• An object thrown straight up with initial velocity magnitude v0 will lose speed according to v(t) = v0 - gt. Thus at some point its upward velocity will become zero and it will fall back, its downward velocity steadily increasing again. If we let it start from d = 0, then d(t) = v0t - (1/2)gt2. Note that d has a very easily found maximum.
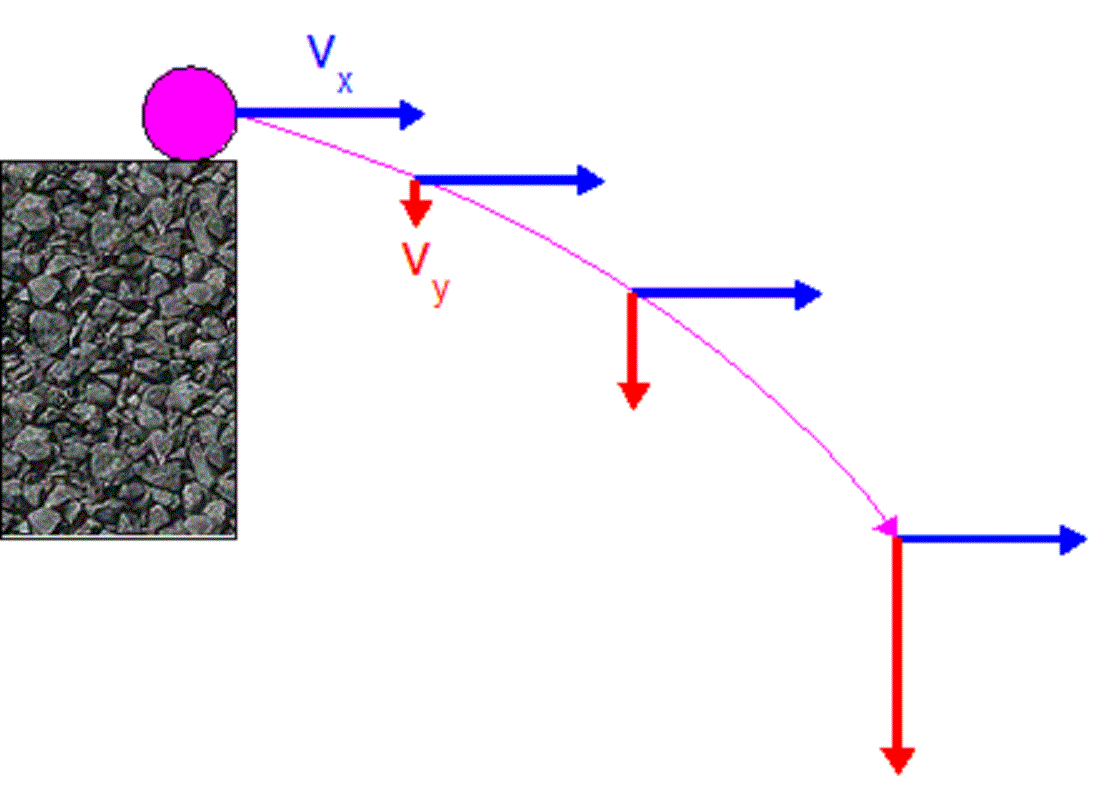
• What if the object is thrown sideways? If we can neglect
the minor resistance presented by the air itself, the
horizontal part of the velocity will never change, but the
originally zero vertical part will continually increase
downward. If we let x be the horizontal direction and
y be the vertical direction then the downward part of
the velocity increases with time like gt and the
horizontal part does not change. That is, vx(t)
= v0 independent of t. But vy(t)
= -gt. The distance fallen downward vertically from the
horizontal line of projection is of course just
d(t) = (1/2)gt2
• PROJECTILES: Conceptually use the vector relation: v(t) = v0 + gt. As for position, r(t) = v0 + (1/2)gt2.
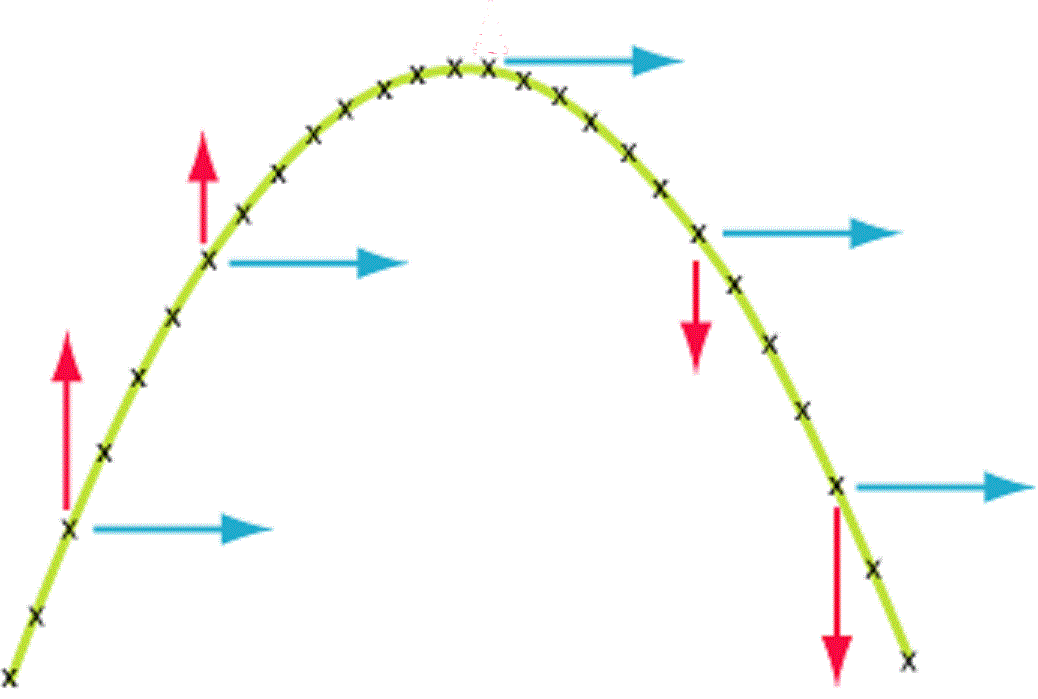
• In all cases, only vertical parts of vectors change with time, because the gravitational acceleration is entirely vertical. Horizontal quantities do not change. Make sure you understand the “Howitzer and Tunnel” and “Monkey and Hunter” demonstrations presented in class!!