|
In a cyclic process, ΔU = 0 and so Q = We. But for the engine, Q = QH - QC. This means that if we define the efficiency as ε = We/QH we find that ε is just 1 - (QC/QH).
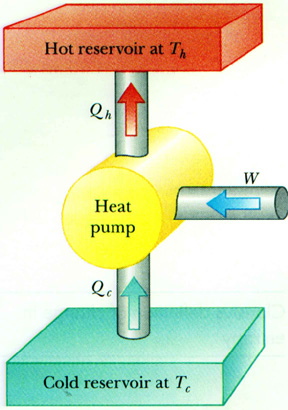
A heat pump takes heat from a low temperature region and dumps it into a higher temperature region.
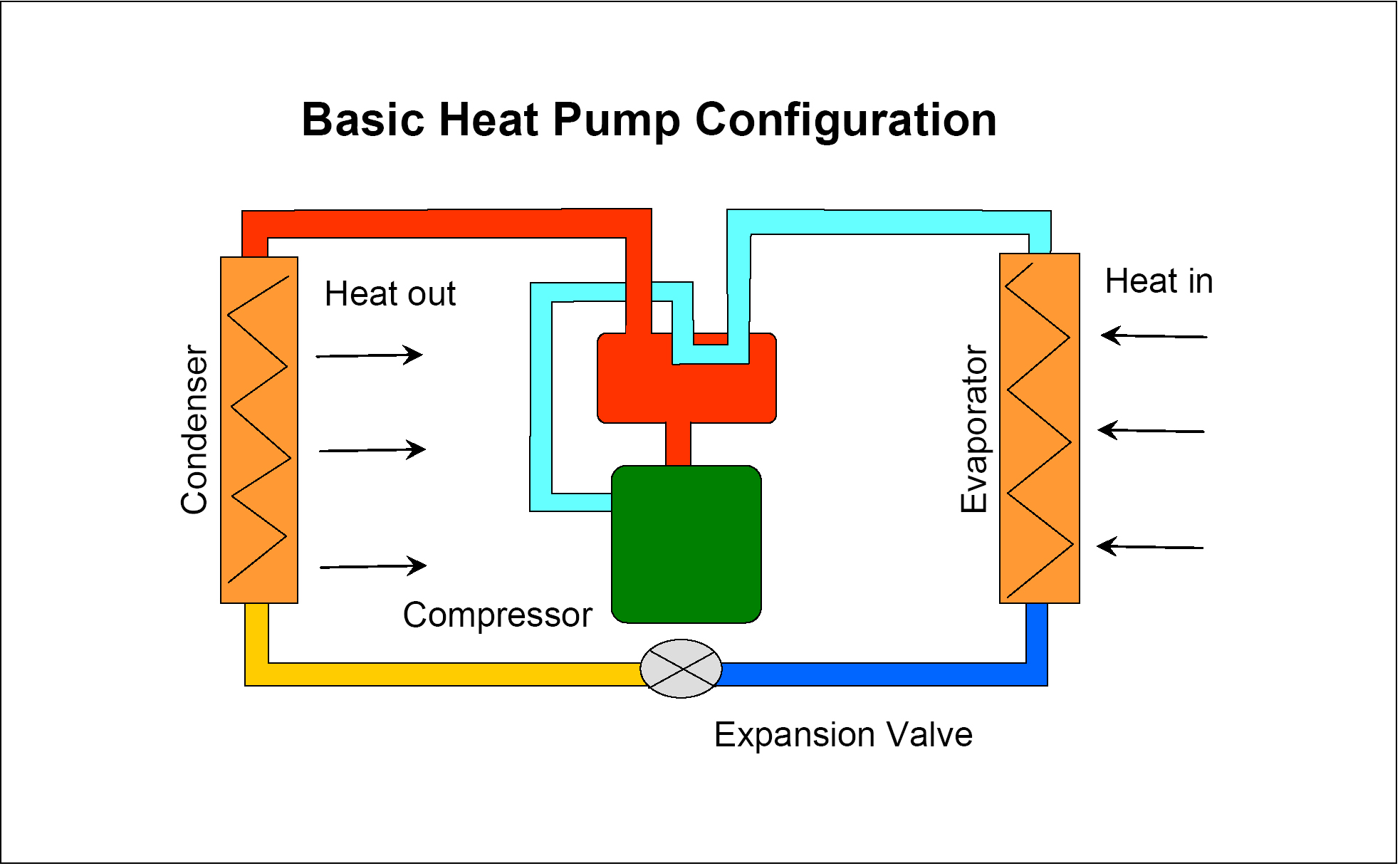
The refrigerator/air conditioner scheme involves vaporizing a liquid in the low temperature region and condensing it in the external world.
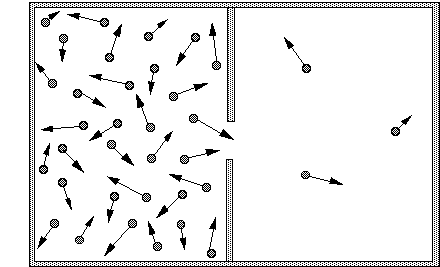
Entropy is a measure of probability. If we make an opening in a container of gas, very quickly there will be the same gas pressure, and the same number of gas molecules, in both new and old regions.
Statistical definition of entropy: S = kBln[Nms].