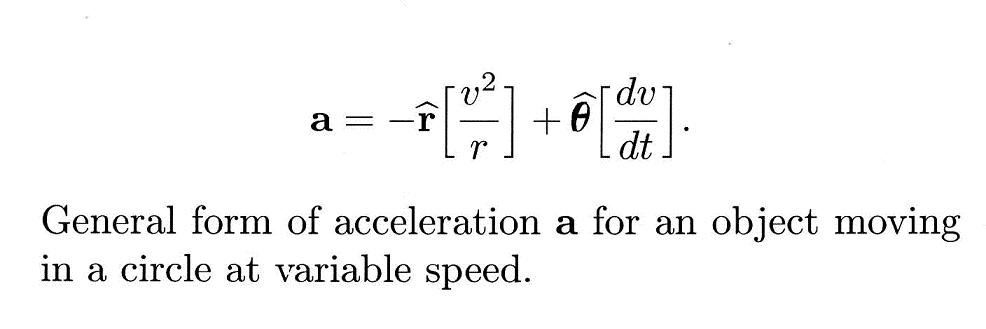
The circular motion has constant speed but continually changing velocity. The acceleration has constant magnitude, but continually changing direction. How do we handle situations where the speed is not constant in the circular motion?

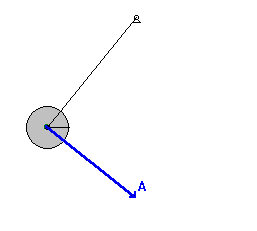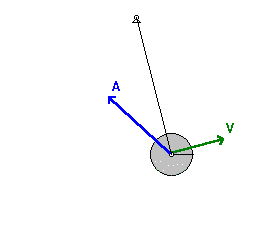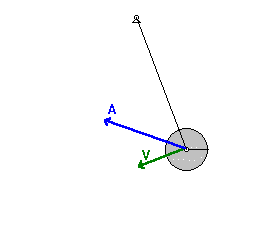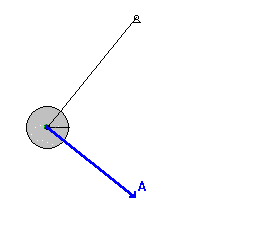
Consider a pendulum. The bob comes to rest on either side of the center line, and its speed is a maximum at the lowest point (along the center line). At first the acceleration is parallel to the increasing velocity, but at the point where the velocity reaches a maximum, the acceleration must be toward the center of the circle. Thus the acceleration of the bob is continually changing in magnitude and direction. How do we analyze it?

We separate the acceleration vector a into two components, the radial acceleration a_r and the tangential acceleration, a_t. The full acceleration is the vector sum of these two components. The radial acceleration is given as usual by the speed squared over the radius of motion, v²/r, while the tangential acceleration is given by dv/dt.