UNCERTAIN UNCERTAINTY?
 |
I have been hanging around
physics departments, for better or worse, in sickness and in
health, in poverty or semi-poverty, as an undergraduate, graduate,
postdoc or faculty member, since 1957.
In all that time I have rarely wavered from my opinion that the only
two “concepts”
of physics the average person has ever heard of are “Einstein's E =
mc
squared”
and “Heisenberg's Uncertainty Relation.”
Here, let's stick to the
Uncertainty Relations (there are actually
many). The average person,
when I inquire, seems to think that Uncertainty in this context means
one or
more of the following:
→ “Scientists don't know
anything for certain, everything is
uncertain.”
→“Scientists can't measure
anything accurately; every measurement gives
an uncertain result, no matter how careful they are.”
→“The precise outcome of
any physical process is never known;
scientists
just have to guess at what has happened.”
and so on...
|
Well, none of these three statements has anything whatsoever to do
with
the Uncertainty Relations of Heisenberg, which are a fundamental
element of quantum
physics, nor do any of these three statements have much, if anything,
to do with science or
with physical reality.
Heisenberg pointed out that many observable quantities in physics
“interfere”
with one another, because the fundamental description provided by
quantum physics
is the probability distribution. To be specific, suppose when we make
measurements over
and over on the same system, always measuring its position along some
axis, we find the
result of each measurement, which can be as precise as we please or can
contrive,
is different from the results of earlier and later measurements. When
plotted as a graph, the
results will usually form a hill-shaped distribution, with some width
Ds.
Now suppose instead of measuring the position of the object, we measure
its velocity.
Again, each measurement can be as precise and accurate as we please or
want to make.
The precision of measurements depends on our care and effort, and
little else.
But again, each time we repeat the measurement, we will get a slightly
different
(but accurate) result. And again, if we plot the results on a graph, it
will form a
hill-shaped distribution with some width Dv.

Now, here is what Heisenberg pointed out. In this case, and many
others, these
observable quantities have distribution widths that are inversely
related.
What we mean is Dv is always proportional to 1 divided by Ds.
So suppose we
do something to our physical system under study, so as to guarantee
that its
position upon repeated measurement varies very little. In other words,
suppose
we try to make Ds as small as possible. This will make Dv
as
large as
possible.
In still other words, if we manipulate the system to make its position
come out
very nearly the same each time we measure it precisely, we pretty much
destroy any information that existed in the system as regards its own
velocity. Or, if
we manipulate the system to make its velocity come out very nearly the
same
each time we measure it precisely, we pretty much destroy any
information
that existed in the system as regards its own position.
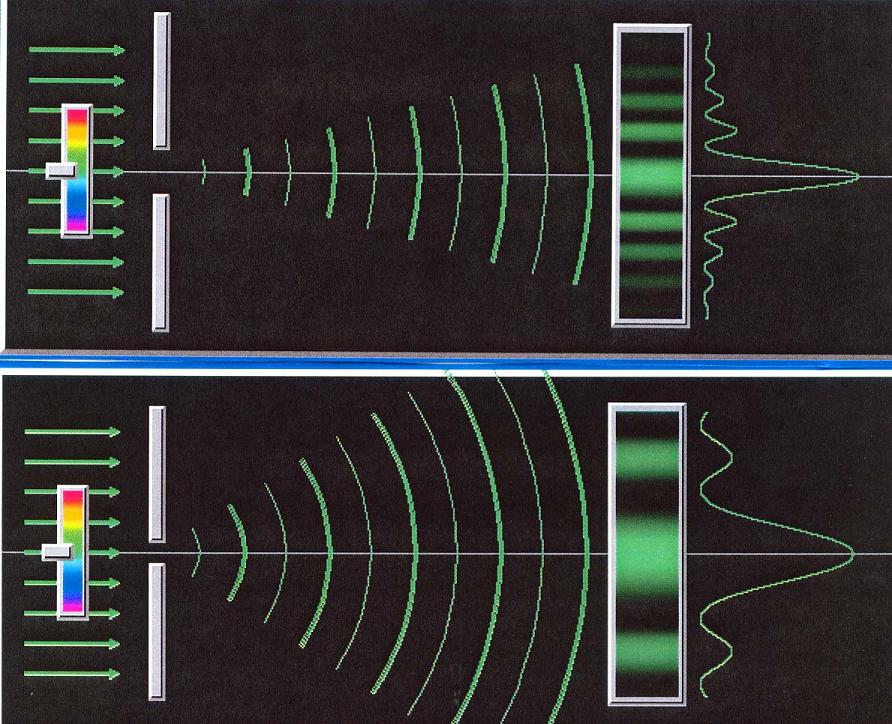
One of the best ways to demonstrate this in class
is to use a laser and an adjustable single slit. Light consists of
particles, called
photons, and each photon in the laser beam has very precisely the same
speed
(the speed
of light!) and direction of motion. Since speed plus direction is
velocity, the
velocity of each photon is very precisely known. Now send the laser
beam through
the adjustable slit, and have the slit wide open. The beam goes through
unaffected; the
velocity information is not disturbed. But now start closing down the
slit. The images
above are a link to a Java applet that will let you do this and see the
result directly.
As you make the slit smaller and smaller, you are more and more
precisely determining
the side-to-side position of the particles in the beam. Narrowing the
slit
narrows Ds. The result is that the distribution of possible velocities
in that
direction becomes greater and greater. As we narrow the slit more and
more, we see the laser beam
spread out more and more along the direction of the slit.
Let's discuss some consequences and
details.
First, you can measure the position of a quantum system as precisely as
you please
and then turn right around and measure the velocity as precisely as you
please.
No problem at all!
What Heisenberg pointed out is that you can't simultaneously
discover the
position and velocity of any quantum system by any imaginable physical
investigation. Another way to put this is that no quantum system
has a trajectory. Another way to put this is that no
information exists in nature as to the simultaneous position and
velocity of a quantum
particle. No quantum system can be in a state where both Ds and Dv
are vanishingly small.
For a historical discussion of the
development of the principle, click here.
It needs to be mentioned that there are many different
“Uncertainty Relations” that exist in
quantum physics and even in classical wave physics. A famous and useful
one relates the
possible spread in values of the total energy of a system, DE,
to the possible spread in values for the time at which some process
occurs in the
system, Dt.
There are uncertainty relations that connect many different observable
physical quantities
to others. In quantum physics, observable quantities are represented by
mathematical
entities called operators. When two different operators have a certain
property
called non-commutation, an uncertainty relation always exists
between
the two different
observable quantities represented by the operators.
Next
Science Page?
 |
One final irony. Whenever
an atom is depicted symbolically, in the media or even in
elementary textbooks, it is invariably depicted as the pre-quantum Bohr
atom
of 1915. In Bohr's semiclassical model, electrons orbited the nucleus
much as planets
orbit the sun. In 1925 it was realized that the one thing electrons and
other subatomic
particles never do is “orbit” anything! Quantum particles have
no
trajectories. Why, then, is the incorrect Bohr model always depicted
instead of a correct,
quantum atom? My guess is that there are two aspects to the continuing
problem: (1) blissful, total ignorance; and
(2) artistic or congenital inability to draw a
probability distribution.
|
 |




