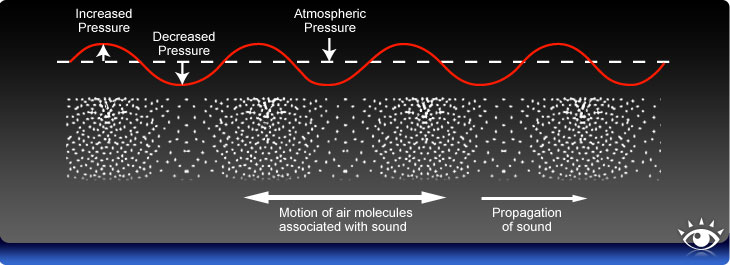
Sound waves in solids or liquids are best viewed as propagating longitudinal disturbances in the density of the material. For sound in a gas, it is easiest to visualize a propagating longitudinal disturbance in the gas pressure.

 |
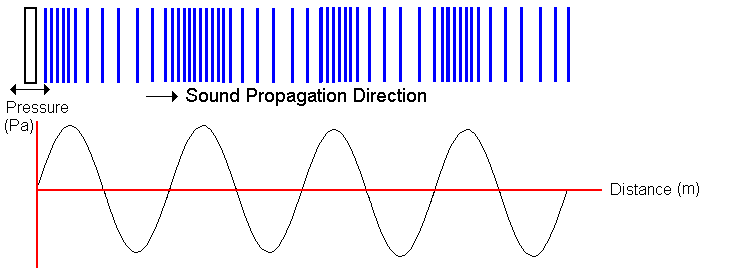
The particle displacement function s(x,t) and the pressure variation function Δp(x,t) are 180 degrees out of phase, so that a zero in one corresponds to a maximum or minimum in the other. In doing Quest problems, note carefully which function is given, or which function is sketched!
If we write s(x,t) = sm cos[kx -ωt], then we get