
 |
The change in gravitational potential energy is defined as the work done against gravity in moving an object from initial to final position. The work depends only on the initial and final positions, not the path taken.
Wg = − ∫ mg · dr, which reduces to Wg = mgy. We define the gravitational potential energy for a constant g therefore to be

Note that since y = 0 can be set anywhere, the zero of gravitational potential energy is completely arbitrary. Therefore it cannot be used unless you specify at what spot it is taken to be zero!!

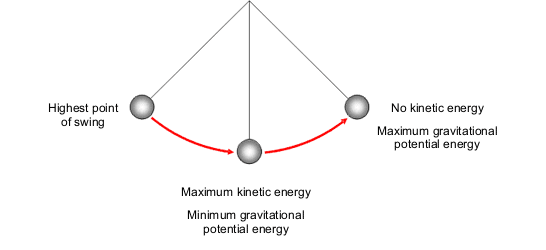
The sum of kinetic energy and potential energy remains constant if no other forces than gravity do work.
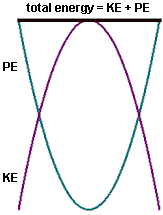
If only one conservative force is doing work, and no non-conservative forces act, then because of the way we have defined KE and PE, whatever dependence the PE U has on position, the dependence of the KE K is guaranteed to mirror it in the opposite sense. Thus E = K + U must be a constant independent of position or any other property of the system.
Since E = K + PE, a point where E = PE is called a classical turning point. And on a plot, for example of PE = (1/2)kx2, it is easy to see graphically what K and PE are, and how they are related, at any value of x.