Nanoparticle Research
at The University of Texas in Austin

Nonlinear Femtosecond Laser Spectroscopy of Nanoparticles
Introduction:
What influences the efficiency for nonlinear optical
devices?
Conversion of light to a different frequency is a wave-wave interaction
process governed by the optical nonlinear coefficient, the "nonlinear
susceptibility" of the material. From the power series expansion of the
susceptibility χ as a function of electric field, usually either the
second order χ(2) or the third order χ(3) term is
employed for practical devices. This yields respectively, processes
that interact 3 waves (second harmonic generation or sum or difference
frequencies of 2 waves) or 4 waves (third harmonic generation,
frequency shifting to the sum or difference of 3 waves, and degenerate
four-wave mixing (FWM) yielding a phase conjugate wave at the same
frequency). Three things are essential in an efficient device: 1) a
large nonlinear coefficient to couple the interacting waves but not
accompanied by significant linear absorption of any of the interacting
waves, 2) a means to keep the generated wave in phase (travelling at
the same phase velocity) with the driving polarization for the
generated wave, produced by the interaction of the source waves, over a
significant interaction length, called "phase matching" and 3) a way to
keep the waves confined transversely through the interaction length by
a wave guiding structure or by focusing, which is limited by
diffraction.
Materials for degenerate nonlinear optics:
It is known that metal and semiconductor nanocomposites have
large nonlinear susceptibilities χ(2) and χ(3). A
nanocomposite of metal nanoparticles has a third-order susceptibility
1,000 times that of bulk materials. For silver (Ag) nanoparticles in
fused silica χ(3) ~ 10-7 esu, nearly 7
orders of magnitude larger than fused silica itself. But, this large
enhancement has only been observed in degenerate four-wave mixing
experiments. The reason for this is that field enhancement is
wavelength specific. In metallic nanoparticles this wavelength is near
the surface plasmon energy, about 3eV in Ag. Because all four waves are
on resonance, field enhancement enters into the nonlinear wave
equations with a high power.
Really, degenerate FWM experiments are less efficient than
what is predicted solely by the susceptibility. The nonlinear
coefficient divided by the linear absorption χ(3)/α
provides a more accurate measure of the overall efficiency. For metal
nanocomposites χ(3)/α ~ 10-12 to 10-11
esu. On the other hand, semiconductors have less loss. Large χ(3)in
semiconductors occurs near conduction to valence band transitions and
can be tuned by choice of the band gap and by the size of the
nanoparticles (e.g. by quantum confinement). This requires a narrow
size distribution of nanoparticles to obtain the largest χ(3).
Our LAM process generates a narrow size distribution.
The limits of field enhancement:
In addition to high absorption, very fast (~10-15)
decoherence and and decay routes have been shown to frustrate
enhancement schemes. Runaway fluorescence losses have been observed in
silver nanoparticles, that may be related to white light generation.
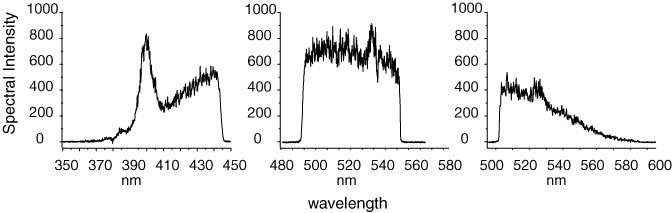
Metal nanoparticles, in particular the noble metals, like Cu, Au, and Ag will fluoresce if they are strongly excited. The fluorescence from these nanoparticles is as efficient, or even more efficient than the harmonics they produce. It is also ultra-broadband. We have performed time-corollated, single photon counting measurements to estimate the fluorescence lifetime in silver nanocomposites formed by LAM. This measurement provided an upper bound on the lifetime, of 162ps.
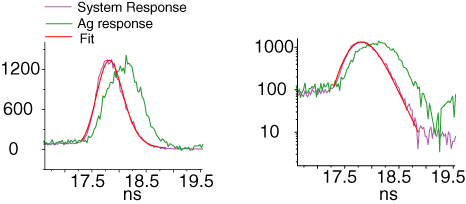
Other measures put the decay even faster, on the order of the femtosecond pulse duration. We are currently developing an ultrafast upconversion lifetime apparatus, to study the ultrafast energy dynamics of silver conduction electrons under intense local field stimulation. Overall, it will help us to understand energy loss pathways, so that field-enhancement mechanisms can be more efficiently designed and implemented.
Non-degenerate nanocomposites for nonlinear optics:
Nonlinear materials to enhance second-harmonic and
third-harmonic generation of a femtosecond laser pulse require new
design principles. An enhanced nonlinear material that resonates the qth
harmonic requires a material that will resonate all the q-1, q-2, ...,
2, 1 subharmonics. It must also satisfy the appropriate symmetry
conditions, set by the particular harmonic order. For instance, second
harmonic generation is more restrictive than third-harmonic generation,
because an asymmetric material is required to satisfy angular momentum
conservation. 2 l=1 photons cannot radiate an l=1 photon without any
additional angular momentum. This is typically accomplished in a
biaxial crystal like Calcite, BBO, or z- cut quartz, but also can be
accomplished using silver nanoparticles.
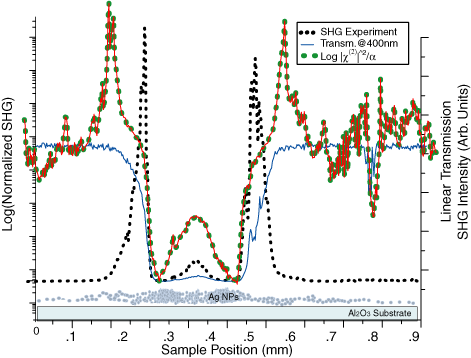
Although perturbation theory predicts third-harmonic generation is a lower efficiency process, it tends to by more efficient. That's because 3 l=1 photons can (and do) combine and stimulate an l=1 photon, without relying on extra help from the surrounding medium. By using different mixtures of nanoparticles, we aim to design materials that are capable of resonating all these subharmonic at once.
Wild, new frontiers:
Our results have shown THG enhancement of femtosecond lasers
may require unique solutions, because of the large group velocity
mismatch between the pump pulse and the harmonic pulse. One effect of
this is that THG is highly interface sensitive. It may be that quasi
phase matching is a naive approach, so enhancing third-harmonic effects
means designing materials materials that will manipulate how pulses
travel in a material. Click here
to open up a .pdf presentation that describes interface THG generation,
and how it is used to study nanocomposite optical materials (5Mb,
Requires Acrobat 6.0).
Interface THG may also become a useful diagnostic for designing subharmonic nonlinear resonators. We are now developing a phase sensitive diagnostic that will allow us to measure the efficiency of each, successive energy step.
Research Goals:
1.The development of efficient, nanoparticle-based nonlinear optical materials for second and third-harmonic generation
2.A better understanding of 'runaway' effects in field enhancement schemes.
3.Optical diagnostics that relate nonlinear performance to electron transport at the nanoscale.