One fairly difficult concept of physics that has been in the news a lot lately is the group velocity of waves, and specifically of light waves. Almost all reports on recent experiments with varying the group velocity of beams of light, as covered in newspapers, or on TV or on the Internet, have been in whole or part total gibberish.

First, let's try to understand the concept of a group velocity with a simple analogy. Consider the scissors at the left of this paragraph. If the scissors are not animated, hit reload to get them to close a few times. Holding a real pair of scissors in your hand as you read this is not a bad idea too! Focus your attention on the blades; open and close them a very, very short distance. Now focus your attention on the point where the blades intersect. You will see that even when the tips of the blades move a negligible distance, the intersection can move for almost the entire length of a blade. The speed of the intersection point is many, many times the speed of a single blade, for most scissors. The intersection point motion is analogous to a group velocity, while the blade motion is analogous to a so-called phase velocity.

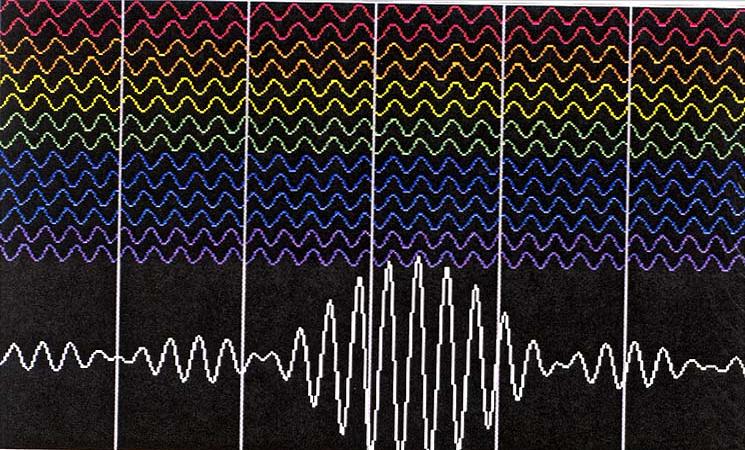
In other words, suppose we are looking at two or more waves, with different frequency and wavelength. If we superimpose the two waves, we will see regions where the two waves add to produce a larger wave, and regions where they almost cancel out. If both waves travel at the same speed, this pattern of "interference" moves along with them. But something very interesting happens if the two waves move at different speeds. Then the pattern moves in a dramatically different way from either wave; it can move much faster; it can move much slower; it can move backward while the waves move forward. The velocity of this pattern is the group velocity. The actual velocity of each wave is its phase velocity. In the animation below, a Moiré pattern is used to illustrate how two waves of different wavelength and speed can interfere to produce a "group" pattern that moves backward compared to either wave, and at a totally different speed!

To really understand any phenomenon in physics, you need to play! Since you are sitting at your computer, a good way to play with group velocity is to play with a group velocity applet, and here is one, and here is another.

Clicking on the slightly cock-eyed image above will take you to another applet that shows (with text explanation included) how a large train of waves of different wavelength can combine to give groups that move faster than any of the waves. Let the applet run awhile and you will see how eventually a large group appears that moves much faster than the actual waves creating it are moving.

If you can figure out how to get each different wavelength of light to move very differently in a special material, you can create a pulse that can have any speed from plus infinity to minus infinity, or that appears to stand completely still!

Over the past 5 years, news media have reported how experimenters constructed a gaseous medium with such properties that when a pulse of light began to enter one side, the same apparent pulse was already leaving the other side, as if moving much faster than light or even violating causality. All that was happening was that the various wavelengths entering the material started moving each at a very different speed (in each case less than the vacuum speed of light), the differences being contrived so that that the original pulse disappeared, while a similar pulse was constructed by superposition among the much-shifted waves that happened to be leaving at the same time the original group was entering. The same thing can be done in reverse; that is, you can contrive the superposition changes so that the pulse entering the material becomes apparently "frozen" in position or moves at a snail's pace. Light that apparently does not move at all is certainly a novelty. Understand, however, that in all these experiments, the light is in a gaseous medium and the phase speed is slower than the speed of light in a vacuum. The interesting effects are due to the fact that each different wavelength moves at a different speed in the medium, the familiar phenomenon of dispersion, which in this case allows the resulting groups to move in very startling ways... startling, anyway, to science-illiterate science reporters. Some writers do a better job, fortunately. Faster than light? Account 1, Account 2. Frozen light? Account 1, Account 2.