2014

Half-metallic magnetism and the search for better spin valves

K. Everschor-Sitte, M. Sitte, and A. H. MacDonald, available online under J. Appl. Phys. 116, 083906 (2014) or arXiv:1407.5240.

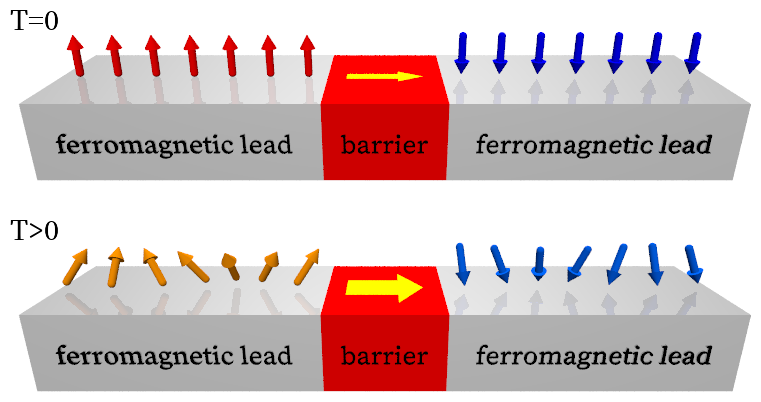
We use a previously proposed theory for the temperature dependence of tunneling magnetoresistance to shed light on ongoing efforts to optimize spin valves. First, we show that a mechanism in which spin valve performance at finite temperatures is limited by uncorrelated thermal fluctuations of magnetization orientations on opposite sides of a tunnel junction is in good agreement with recent studies of the temperature-dependent magnetoresistance of high quality tunnel junctions with MgO barriers. Using this insight, we propose a simple formula which captures the advantages for spin-valve optimization of using materials with a high spin polarization of Fermi-level tunneling electrons, and of using materials with high ferromagnetic transition temperatures. We conclude that half-metallic ferromagnets can yield better spin-value performance than current elemental transition metal ferromagnet/MgO systems only if their ferromagnetic transition temperatures exceed \(\sim 950~\mathrm{K}\).

Real-space Berry phases: Skyrmion soccer

K. Everschor-Sitte and M. Sitte, available online under J. Appl. Phys. 115, 172602 (2014) or arXiv:1405.0987.

Berry phases occur when a system adiabatically evolves along a closed curve in parameter space. This tutorial-like article focuses on Berry phases accumulated in real space. In particular, we consider the situation where an electron traverses a smooth magnetic structure, while its magnetic moment adjusts to the local magnetization direction. Mapping the adiabatic physics to an effective problem in terms of emergent fields reveals that certain magnetic textures, skyrmions, are tailormade to study these Berry phase effects.

2013

Interaction effects on almost flat surface bands in topological insulators

M. Sitte, A. Rosch, L. Fritz, available online under Phys. Rev. B 88, 205107 (2013) or arXiv:1305.1788.

We consider ferromagnetic instabilities of two-dimensional helical Dirac fermions hosted on the surface of three-dimensional topological insulators. We investigate ways to increase the role of interactions by means of modifying the bulk properties which in turn changes both the surface Dirac theory and the screening of interactions. We discuss both the long-ranged part of the Coulomb interactions controlled by the dimensionless coupling constant \(\alpha = e^{2}/(\hbar \epsilon v_{F}^{\mathrm{surf}})\) as well as the effects of local interactions parametrized by the ratio \(U_{\mathrm{surf}}/D_{\mathrm{surf}}\) of a local interaction on the surface \(U_{\mathrm{surf}}\) and the surface bandwidth \(D_{\mathrm{surf}}\). If large compared to 1, both mechanisms can induce spontaneously surface ferromagnetism, thereby gapping the surface Dirac metal and inducing an anomalous quantum Hall effect. We investigate two mechanisms which can naturally lead to small Fermi velocities \(v_{F}^{\mathrm{surf}}\) and a corresponding small bandwidth \(D_{\mathrm{surf}}\) at the surface when the bulk band gap is reduced. The same mechanisms can, however, also lead to an enhanced screening of surface interactions. While in all considered cases the long-ranged part of the Coulomb interaction is screened efficiently, \(\alpha \lesssim 1\), we discuss situations where \(U_{\mathrm{surf}}/D_{\mathrm{surf}}\) becomes parametrically large compared to 1, thus inducing surface magnetism.

2011

Topological insulators in magnetic fields: Quantum Hall effect and edge channels with non-quantized \(\theta\)-term

M. Sitte, A. Rosch, E. Altman, L. Fritz, available online under Phys. Rev. Lett. 108, 126807 (2012) or arXiv:1110.1363.

We investigate how a magnetic field induces one-dimensional edge channels when the two-dimensional surface states of three-dimensional topological insulators become gapped. The Hall effect, measured by contacting those channels, remains quantized even in situations where the \(\theta\) term in the bulk and the associated surface Hall conductivities, \(\sigma_{xy}^{S}\), are not quantized due to the breaking of time-reversal symmetry. The quantization arises as the \(\theta\) term changes by \(\pm 2 \pi n\) along a loop around \(n\) edge channels. Model calculations show how an interplay of orbital and Zeeman effects leads to quantum Hall transitions, where channels get redistributed along the edges of the crystal. The network of edges opens new possibilities to investigate the coupling of edge channels.

2008

Emergent Lorentz symmetry with vanishing velocity in a critical two-subband quantum wire

M. Sitte, A. Rosch, J. S. Meyer, K. A. Matveev, M. Garst, available online under Phys. Rev. Lett. 102, 176404 (2009) or arXiv:0811.4579.

We consider a quantum wire with two subbands of spin-polarized electrons in the presence of strong interactions. We focus on the quantum phase transition when the second subband starts to get filled as a function of gate voltage. Performing a one-loop renormalization group analysis of the effective Hamiltonian, we identify the critical fixed-point theory as a conformal field theory having an enhanced SU(2) symmetry and central charge 3/2. While the fixed point is Lorentz invariant, the effective “speed of light” nevertheless vanishes at low energies due to marginally irrelevant operators leading to a diverging critical specific heat coefficient.

Diploma and Ph.D. thesis

Quantum Hall Effect and Surface Criticality in 3D Topological Insulators

Ph.D. thesis by Matthias Sitte (Köln, 2012), download an electronic copy (PDF).

Topological insulators are unique quantum states of matter. Although they behave like ordinary insulators in the bulk, states involving massless Dirac fermions at the surface of such materials are found to be metallic. Since their discovery in two-dimensional HgTe quantum wells, topological insulators have been very actively studied, both experimentally and theoretically.

In this thesis, we investigate how a magnetic field induces one-dimensional edge channels when the two-dimensional surface states of three-dimensional topological insulators become gapped. The Hall effect, which can be measured by contacting those edge channels, remains integer-quantized even when the topological \(\theta\)-term in the bulk (and the associated surface Hall conductivities \(\sigma_{xy}^{\mathrm{surf}}\)) are not quantized due to time-reversal symmetry breaking. We show that the quantization of the Hall conductivity \(sigma_{xy}^{\mathrm{Hall}}\) arises as the \(\theta\)-term changes by \(\pm 2 \pi n\) along a loop around \(n\) edge channels. Analytical calculations on a model based on strained HgTe are presented, which show how the interplay of orbital and Zeeman effects leads to quantum Hall transitions where channels get redistributed along the edges of the crystal. This network of edges, the existence of which we confirm by numerical tight-binding calculations, opens up new possibilities to investigate the coupling of edge channels.

In the last part of this thesis, we investigate whether long-ranged Coulomb interactions, controlled by the dimensionless coupling constant \(\alpha = 1/(\hbar \epsilon v_F^{\mathrm{surf}})\), can induce spontaneous symmetry-breaking on the surfaces of a three-dimensional topological insulator, thereby creating a gap in the metallic surface states. This would allow an anomalous quantum Hall effect without explicitly breaking time-reversal invariance, i.e., without the application of an external magnetic field. We find that one prerequisite for observing this effect is to reduce the Fermi velocity \(v_F^{\mathrm{surf}}\) of the surface Dirac fermions. However, we find that screening due to bulk metallic states renders the effective interaction strength \(\alpha\) small instead of large and therefore prevents chiral symmetry breaking. We confirm this scenario by explicit numerical tight-binding calculations for various models in slab geometries, and by an analytical calculation of the corresponding polarization functions. We also derive topological criteria for the existence of flat surface bands and discuss under which conditions short-ranged Hubbard interactions may lead to an interaction-induced band gap in the surface states. In particular, we find a generic scenario for a surface band gap due to local interactions in the Fu-Kane-Mele model.

Quantum Criticality at a Conductance Plateau Transition in a Quantum Wire

Diploma thesis by Matthias Sitte (Köln, 2008), download electronic copy (PDF).

In this thesis, we present a theoretical study of interacting spinless electrons in a two-band quantum wire. While the lower band is described as a Luttinger liquid with gapless density excitations, the upper band is modelled in terms of fermions at the bottom of the band. In addition to the usual density-density interaction between the two bands, we investigate the possibility of transferring of pairs of electrons from one subband to the other.

We perform a renormalization group analysis around the strong coupling fixed point, calculating the self-energy and vertex corrections. We then consider the renormalization of the theory with complementary renormalization conditions. As a main result, we find that the interactions between the two bands can lead to a modification of the dispersion relation.

Finally, we focus on the thermodynamical properties of the model. A calculation of the specific heat coefficient is presented in both the non-interacting and interacting system. It is shown that in the presence of interactions the activation of the second band, and the subsequent quantum phase transition, strongly influences the thermodynamics.