| Higher Dimensions in Physics and Mathematics! |
Pseudoscientists lean heavily on the assumption that their readers will know absolutely nothing about science or math. This is a pretty safe assumption, alas. And it requires no effort on the part of the pseudoscientist, because he also invariably knows no science or math either.
It is worth summarizing the ways in which the various concepts of "higher dimensions'' gradually diffused out from legitimate math and science, through hundreds of increasingly distorted, confused and muddled journalistic presentations and sensationalizations, into late 19th Century science fiction and 20th Century pseudoscience.
 |
In the late 19th Century mathematicians became increasingly interested in the foundations of geometry. Our own universe has 3 space dimensions. But what would geometry be like if there were 4 space dimensions? Or 5? Or 10? Or an arbitrary number? Or an infinite number? Mathematicians worked a great deal on geometries with arbitrary numbers of space dimensions. |
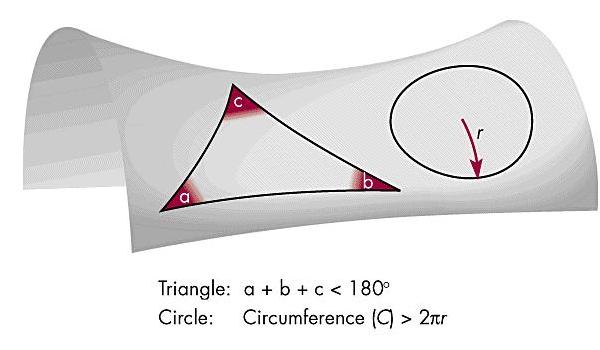
Mathematicians also worked a great deal on "non-Euclidian'' geometries that violate one or more of the postulates of Euclid. In Euclidian geometry, parallel lines remain the same distance apart. One can imagine a geometry in which parallel lines eventually intersect, and a geometry in which parallel lines gradually separate further and further. Such spaces are usually described as "curved''— an example is the 2-dimensional surface of a sphere, on which lines initially parallel at the equator of the sphere intersect at the poles of the sphere.
 |
Mathematicians had no idea that their work would ever prove useful to physicists, but some of it did have application in the real world. For hundreds of years physicists had worked in a 4-dimensional framework, because it takes a minimum of 4 numbers to specify an event: 3 to specify its space location and 1 to specify when it happened. In 1905 Einstein found that, to be correct, laws of physics must be written in a 4-dimensional form that physicists call "Lorentz Invariant,'' or "Manifestly Covariant.'' The reason is that different observers will disagree as to how much of an event "projects'' onto the space axes and how much "projects'' onto the time axis. That is, different observers can disagree as to how long a process takes, or on the size of the physical space that the process occupies. Only the full four-dimensional aspects of the process remain the same for all observers. |
|
In 1915, Einstein found a more general description of gravitational phenomena, in which the density of matter directly determines the "curvature'' of 4-dimensional space-time. That is, his theory of gravity was purely geometrical. The amount of matter determines the type of geometry that exists in the surrounding space. Other matter travels along the straightest possible trajectory in this curved space-time. |
Later, physicists like Kaluza and Klein and Pauli tried to generalize Einstein's ideas to include the electromagnetic force. In order to include a number for "charge,'' the source of electromagnetic effects, in a purely geometrical theory, they had to add a new space dimension, since every number in a geometrical theory is a projection onto a coordinate. Thus, they wound up with a 5-dimensional theory (4 space dimensions, and time). These so-called Kaluza-Klein theories did not seem to lead anywhere, and were abandoned.
 |
Physicists for centuries have worked in arbitrary spaces, usually called "phase space,'' in which various important physical quantities are interpreted as dimensions. For instance, in order to show the "state'' of a container of gas, one might plot a graph in 3 dimensions, the 3 dimensions being pressure, volume and temperature. To show the "state'' of a particle, a physicist might plot 4 dimensions, 3 of them being the 3 components of the momentum vector of the particle, and 1 being time. If it requires 100 numbers to specify a process, then a graphical description of the process would have to show "slices'' through a space of 100 dimensions. None of these would be required to have anything to do with actual space dimensions. |
|
In the late 1920s, physicists working on quantum physics found that the mathematics fell naturally into the framework of a theory of vectors in a space with a denumerably infinite number of dimensions. German mathematician David Hilbert had already worked out the theory of such spaces, which we call Hilbert Spaces. In quantum physics, each possible outcome of a measurement is a projection along an axis in an abstract space, having nothing to do with space-time. A bit later British physicist P. A. M. Dirac pointed out that in general the space used in quantum physics needs an indenumerably infinite number of dimensions. The mathematics of such a space remained unknown and unacceptable to mathematicians for 4 decades, until a Russian mathematician named Gel'fand worked out the rules of what he called "rigged Hilbert space.'' This did not in any way retard physics or physicists, who are used to inventing the math they need as they go along, rather than waiting for mathematicians to decide that such math does exist and name it. They were working in spaces with indenumerably infinite dimension long before mathematicians ever imagined the concept, just as Isaac Newton invented calculus to do physics, before mathematicians ever heard of it. |
 |
Multidimensional spaces have even proved useful in computer architecture. For example, networks of processors can be set up that are linked geometrically as surfaces would be in a multidimensional space.

The structure of all known physical laws demands that our universe have only 3 extended space dimensions. For example, the fact— established and confirmed by experiment consistently for nearly 400 years— that all long-range interactions, such as gravity and the radiation field of the electromagnetic force, fall off like the inverse square of the distance, demands that space be precisely 3 dimensional.
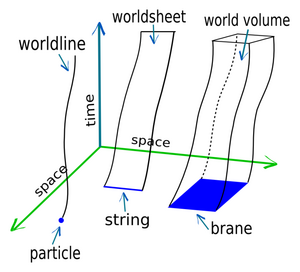
More confusion about higher dimensions was generated in the press beginning in 1984, when physicists became excited about so-called "string theory.'' Physicists have never been able to work out a theory of gravitation that is consistent with quantum mechanics and also has some feature that indicates it might be uniquely correct! String theory provided a geometrical description of quantum processes that incorporated gravity very naturally. But three other forces besides gravity are known. Borrowing the idea of Kaluza and Klein, physicists incorporated the other three forces and their "couplings" by adding space dimensions— the only thing you can do in a theory that is purely geometric. A typical string theory had 9 or 10 space dimensions and 1 time dimension. The extra space dimensions had to be there to incorporate phenomena other than gravity geometrically, but they could not "actually'' be there or the theory would not have worked. The solution was to curl these extra dimensions up mathematically into tight "wads'' no more than 10-35 meters in length, a process called "compaction." The extra dimensions would thus be "compact," and indetectable. At first it was hoped that such a theory would be unique, so that we would have confidence that this was the right way to go. After nearly 25 years, the "glitz'' of string theory has almost entirely worn off. Midway along, physicists began to realize that the five or six different string theories that had been suggested all appeared to be different limiting cases of a far more general theory, which is tentatively called "M-Theory." In M-Theory, strings are generalized into surfaces and membranes, and ordinary space-time coordinates no longer exist in general. The space-time framework can still be up to eleven-dimensional. It is vital to realize that no aspect whatsoever— not even the most basic assumptions— of string theory has ever been tested experimentally. Only in early 2007 was an experimental test of of its three basic assumptions finally proposed.
|
So far, physicists have no concrete idea as to what a unified theory of all quantum processes and gravity might look like, but it is certainly possible that such theories will remain multi-dimensional. It is important to realise that these theories have absolutely no contact with experiment at present. There is no experimental evidence of any kind whatsoever for dimensions beyond the usual four. Physicists over the past decade (say 2002 up to now) have been working on many wildly different approaches. In one approach, six extra dimensions above four remain extremely compact, to agree with experiment. In another promising class of approaches, there are up to 11 dimensions, and at least one is "extended" rather than "compact," but all interactions except gravity are "trapped" on a "4-brane," the ordinary 4-dimensional space-time we actually live in. This leads to the concept of multiple "brane-worlds," parallel universes that physics forever keeps separate... unless they collide! At a minimum, it seems at least one extra extended dimension is needed, making four of space and one of time, to solve the various conundrums that particle physics faces. |
 |
 |
Harvard physicist Lisa Randall, in her book Warped Passages, fairly lucidly explains the various problems that have arisen in trying to understand the physics of fundamental particles and processes, and how adding one or more extra dimensions can reduce aspects of nature, seemingly impossible to explain, down to fairly straightforward and possible situations that are just on the verge of testability. One straightforward tipoff that extra dimensions are there would be a departure of the gravitational force from the familiar inverse-square dependence on distance, for small distances. How small? Well, indeed gravity has not been very carefully studied and probed at very short but macroscopic distances, such as 10-5 meters or less. Fairly simple but tedious experiments can be done and are being done to settle some of these questions, and we will just patiently have to await results. As for the theoretical situation, it changes almost monthly, as theorists make suggestions about M-Theory, quantum theories of gravity based on string theories, quantum theories of gravity independent of string theory, various multidimensional extensions of the Standard Model of particles and forces, and the like. |
A lesser-known alternative to string theory, which also provides a possible quantum theory of gravity, is so-called Loop Quantum Gravity. In this approach, first suggested at about the same time as the earliest string theories [mid-1980s], space-time is four dimensional but has a “grainy,” discrete structure at submicroscopic levels. At present (2011), loop quantum gravity still remains a very viable alternative to string theory, and some have suggested that the two different approaches might turn out to be different approximations to a single, more general theory.
In any case, no matter what new ideas and new information are forthcoming along these lines in the future, the statement that there are only three extended space dimensions available to macroscopic objects such as ourselves will remain true no matter how M-Theory or quantum gravity or whatever replaces them ultimately may develop, or what experimenting at scales of energy and distance we haven't examined in detail before ultimately reveals to us. Theories try to describe the world, they don't change it. Elephants don't lay eggs. Facts is facts.
Beginning in the last decade of the 19th Century, newspapers and magazines were full of completely confused accounts of "the fourth dimension,'' not to mention "vibrations'' and "energy,'' two hot topics of late 19th Century physics. When Einstein came along, the "fourth dimension'' became an even hotter topic, and acquired some curves too. Higher dimensions in pseudoscience are often even further confused with then-unrelated scenarios, such as "coexistent worlds,'' "parallel worlds,'' the "worlds'' reached in dreams and drug-visions, not to mention Heaven, Hell, and even other planets. Mindless journalistic publicity for string theories has over the past two decades touched off yet another wave of science-fictional and fantastical delirium involving "multiple universes," a delirium owing a lot to late 19th Century Theosophy, but essentially nothing whatsoever to advances in physics.
Pseudoscientists and fiction writers have always loved "higher dimensions.'' Almost any fantasy can be motivated by appeal to the "mysterious 4th dimension,'' or the famous "15th Akasic dimension.'' But it is important to realize that such concepts are not borrowed from either science or mathematics, and have no basis whatsoever in the verified descriptions and observed phenomena of the world we actually live in.
 |
 |
Create your own four-dimensional creatures here, seen only as two-dimensional slices as you interfere with the natural evolution of a pocket universe... or so it says.
For further reading: