Homework for PHY 309L
Welcome to homework assignments for the Elementary Physics (II)
course, PHY 309 L.
The homeworks on this page are for the section taught by
Professor
Vadim Kaplunovsky in Fall 2014 (unique #57915).
Other sections assign different homeworks.
Many homework problems are taken from the Griffith and Brosing
textbook; such problems are listed by chapters and numbers,
for example Q2 at the end of chapter 13.
Please note the letter in the beginning of each number: Q2, E2, and SP2 are
different problems.
Also, the numbers are according to the 7th edition;
if you use an older or a newer edition, the number in your book will be different.
In addition to the textbook problems, I will make some problems of my own, or copy
problems from other books.
All such non-textbook problems will be written down on this page.
For grading purposes, the harder problems will be worth more points than the easier problems.
The pointage will be shown after each problem;
if the pointage is not shown, the problem is worth 10 points.
Please note that the physical laws and the formulae you use
and the way you put them together are more important for your grade
than the numbers you calculate.
If you understand the physics governing a problem, use correct formulae,
and properly put them together, you would get a high partial score even
if your arithmetic is faulty.
But you would get a low score for a numerical answer without a clear explanation of
where it came from, even if the number happens to be correct.
I shall collect the homeworks in class on the due date.
If miss the class that day, scan your homework and email me the scan before the end of the day.
If you do not have a scanner, take a picture with your digital camera or cellphone,
and make sure the picture is readable.
If you do your homework as a team, please turn in a single copy with all your names on it;
don't waste the TA's time with multiple copies.
And make sure all members of the team understand all the problems.
Schedule of Homeworks and Exams.
| Set | Assigned | Due | Chapter(s) |
|---|
| Set 1 | August 27 | September 5 (Friday) | 12 |
| Set 2 | September 5 | September 12 (Friday) | 12, 13 |
| Set 3 | September 12 | September 19 (Friday) | 13, 14 |
| Set 4 | September 19 | September 29 (Monday) | 14 |
| Midterm 1 | October 1 (Wednesday) | 12, 13, 14 |
| Set 5 | October 1 | October 8 (Wednesday) | 14, 15 |
| Set 6 | October 8 | October 15 (Wednesday) | 15, 16 |
| Set 7 | October 15 | October 22 (Wednesday) | 16 |
| Set 8 | October 22 | October 29 (Wednesday) | 17 |
| Midterm 2 | October 31 (Friday) | 15, 16, 17 |
| Set 9 | October 31 | November 7 (Friday) | 17, 18 |
| Set 10 | November 7 | November 14 (Friday) | 18, 19 |
| Set 11 | November 14 | November 21 (Friday) | 18, 19, 20 |
| Midterm 3 | November 24 (Monday) | 17, 18, 19 |
| Set 12 | November 24 | December 5 (Friday) | 20 |
| Final Exam | TBA | everything |
Each homework set should be posted by the "assigned" date in this schedule.
If it is not, let me know ASAP.
The textbook chapters in the schedule are tentative.
They may change if the class goes faster or slower than I expect.
Exams
Homework sets
Set 1
Textbook questions Q4 [8 pt], Q14, Q23 [12 pt]
and problems E8, E10, E12,
and SP1 [15pt] at the end of chapter 12.
One non-textbook problem:
- [12 pt] (a) Four electric charges are placed at the corners of square ABCD with 20 cm sides.
The charges at the two upper corners A and B are positive,
qA=qB=+0.10 μC,
while at the bottom two corners C and D the charges are negative,
qC=qD=−0.10 μC.
Find the electric field vector — both the magnitude and the direction —
at the center of the square.
(b) Now let's replace the positive charges at corners A and B with equal and opposite negative charges
so that all 4 charges are equal,
qA=qB=qC=qD=−0.10 μC.
Find the new electric field vector at the center of the square.
Hint: Use symmetry of the configuration.
Update 8/31: The non-textbook problem I is postponed to the next homework.
Due September 5; solutions.
Set 2
First, three non-textbook problems:
- [12 pt] (a) Four electric charges are placed at the corners of square ABCD with 20 cm sides.
The charges at the two upper corners A and B are positive,
qA=qB=+0.10 μC,
while at the bottom two corners C and D the charges are negative,
qC=qD=−0.10 μC.
Find the electric field vector — both the magnitude and the direction —
at the center of the square.
(b) Now let's replace the positive charges at corners A and B with equal and opposite negative charges
so that all 4 charges are equal,
qA=qB=qC=qD=−0.10 μC.
Find the new electric field vector at the center of the square.
Hint: Use symmetry of the configuration.
- In old-style TV tubes and computer monitors, the picture on the screen was produced by electrons beams
striking the back of the screen at high speeds.
The electrons were emerging from a hot cathode (hence the name cathode ray tube (CRT) for the monitor)
with negligible speeds, but then were accelerated to high speeds by big voltages between the cathode and
the other electrodes.
Suppose the cathode has negative electric potential −2500 volt,
while the screen (which acts as the anode) has zero electric potential.
With what speed do the electrons strike the screen in this monitor?
Use energy conservation to answer this problem.
For your information, every electron in the Universe has charge
qe=−e=−1.60·10−19 C
and mass me=9.11·10-31 kg.
- Consider a capacitor made out of two parallel metal plates of area
A=0.64 m2 separated by an air gap of thickness d=4.0 mm.
(a) Suppose the voltage (i.e., potential difference) between the two plates is 9600 volts.
What is the electric field between the plates?
(b) What electric charges should the two plates have in order to create such a field?
(c) What is the capacitance (charge/voltage ratio) of this capacitor?
(d) How much electric energy is stored in this capacitor?
Next, three texbook questions Q1 [6pt], Q7 [6pt],
and Q10 at the end of chapter 13.
Finally, one more non-textbook problem.
- [16 pt] Three light bulbs are connected in parallel to a 3.0 volt battery.
(a) Draw the circuit diagram.
(b) Each bulb has resistance R=6.0 Ω.
Find the electric current flowing through each bulb.
(c) Find the net current flowing through the battery.
(d) Find the net resistance of the parallel 3-bulb circuit.
(e) Now let's connect the same 3 light bulbs in series to a 6.0 volt battery.
Draw the new circuit diagram.
(f) What's the potential difference (ie, the voltage) across each bulb?
(g) Find the current flowing through each bulb, and also the current through the battery.
(h) Find the net resistance of the series 3-bulb curcuit.
Due September 12; solutions.
Set 3
Non-textbook problems:
- Consider two resistors, R1=10.0Ω and R2=15.0Ω.
(a) What would be the net resistance of these two resistors connected in series?
(b) What would be the net resistance of these two resistors connected in parallel?
- At room temperature, copper has resistivity ρ=17·10-9Ω m.
Calculate the resistance of a copper wire of diameter 2r=1.0 mm and length L=1.6 km
(1 mile).
Texbook problems E8, SP4 (15pt),
Q22, E15, and SP5 (12pt)
at the end of chapter 13.
Textbook questions Q4 and Q5
at the end of chapter 14.
Due September 19; solutions.
Set 4
Textbook questions and problems Q8 (8pt), SP1 (12pt),
SP2 (12pt), Q26, and E12
at the end of chapter 14.
Non-textbook questions: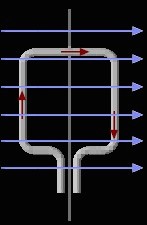
- (15 pt) A current-carrying loop of wire is placed in the magnetic field as shown on the right.
The loop can rotate around the vertical axis, but right now it's parallel to the plane of your screen.
The magnetic field points horizontally to the right.
(a) What are the directions of the magnetic forces on each segment of the loop?
(b) Is there a net torque on the loop? If yes, which way is it going to turn?
(c) Now let the loop spin around the vertical axis, while the current keeps flowing
in the same direction.
What happens to the torque on the loop while it's turning?
(d) What should one do to make sure the torque on the loop stays in the same direction
while it spins?
- (12 pt) A flat coil of wire rotates around a horizontal axis (through the plain of the coil itself)
in a vertical magnetic field.
When the coil happens to face up, the magnetic flux through the coil is +2.5 Vs, when the coil
faces down, the flux is −2.5 Vs, and when the coil happens to be vertical, the flux is zero.
(a) The coil rotates at uniform rate of f=60 revolutions per second,
so the angle between the coil and the vertical depends on time as φ=2πft.
Argue that the flux through the coil depends on time according to
Φ(t)=Φmax×sin(φ)=Φmax×sin(2πft)
for Φmax=2.5 Vs.
(*) Mathematical note: this function changes with time at the rate
δΦ/δt=(2πf×Φmax)×cos(2πft).
(b) Write down the voltage (or rather the electromotive force)
induced in the rotating coil as a function of time.
(c) What is the amplitude of this AC voltage?
- (12 pt) The primary coil of a transformer has 720 turns of wire while the secondary coil has only 24 turns.
For simplicity, assume a perfectly efficient transformer.
(a) The primary coil is connected to AC power at 120 V (effective).
What is the (effective) voltage on the secondary coil?
(b) The AC current through the secondary coil is 15 A (effective).
What is the current flowing through the primary coil?
(c) How much power does this transformer transmit from the primary coil to the secondary coil?
(d) Now consider a different transformer, with different nunmbers of turns in each coil.
This transformer heats up when used, which indicates poor efficiency:
some of the electric power going through this transformer turns into heat.
If the AC voltage on the primary coil of this transformer is 120 V, the voltage on
the secondary coil is 2.4 V, and the current through the secondary coil is 20 A,
what can you say about the current through the primary coil?
Due September 29 (Monday); solutions.
Set 5
First, a couple of non-textbook problems:
- (15pt) Corrected 10/7 at 4:20 PM.
One of the demos I have showed in class had a metal ring jumping almost to the ceiling because of
magnetic forces on eddy currents induced in the ring.
Suppose the ring is horizontal (i.e., its axis is vertical) while the magnetic field is directed
mostly vertically up but also has a smaller horizontal component away from the ring's axis.
The average vertical field through the ring increases with time at the rate
ΔBz/Δt=120 T/s, while the horizontal outward field also
increases with time but at a smaller rate.
The ring itself has radius r=2.5 cm and electric resistance R=0.40 mΩ (to the
current flowing around the ring).
(a1) Find the voltage (or rather the electromotive force) induced in the ring.
(a2) Find the eddy current flowing through the ring.
(b) Use Lenz rule to find the direction of the eddy current.
(c) Show that for each piece of the ring, the magnetic force on the eddy current has both a
horizontal and a vertical components; the horizontal component is directed to the center of the ring
while the vertical components pushes the ring up.
(d) Calculate the net upward force on the ring at the moment when the horizontal radial component of the
magentic field (at the ring's location) reaches Br=0.15 T.
- Joe hold one end of a rope in his hand while the other end is tied to the wall.
Joe pulls on the rope giving it a steady tension, while at the same time his hand moves up and down,
which makes waves on the rope.
(a) Suppose Joe start moving his hand at higher frequency while pulling on the rope with
the same steady force, so the speed of the waves does not change.
What happens to the wavelengh? Does it become shorter or longer?
(b) Now suppose Joe keeps the same frequency but increases the rope's tension, which
makes for a higher speed of the waves.
What happens to the wavelength in this case? Does it it become shorter or longer?
In both parts, please explain your answer.
Next, textbook problem E4 and questions Q16 (7pt)
and Q17 at the end of chapter 15.
Finally, 2 more non-textbook problems:
- You are listening to a radio which has two speakers; each speaker gets the same electric signal,
but they are located in different corners of your room.
You have a remote which can turn the speakers on or off independently from each other without
moving your head, which happens to be
3.2 meters from one speaker and 3.6 meters from the other speaker.
(a) Suppose the sound waves produced by the speakers has wavelength λ=40 cm.
Is the interference between the two speakers is constructive or destructive?
What is the power of the combined sound compared to the power of a single speaker?
(b) If the savelength changes to λ=80 cm, would the interference
be constructive or destructive?
What would be the power of the combined sound compared to the power of a single speaker?
- Two out-of-tune musical instruments try to play the same note — middle C —
but the sounds they produce have slightly different frequencies,
f1=261 Hz and f2=264 Hz.
(a) Explain why playing these two instruments at the same time produces beats.
(b) Calculate the beat frequency: how many times does the sound intensity go up and down
in one second.
Due October 8 (Wednesday); solutions.
Set 6
First, question Q20 and problem SP2 (15 pt)
at the end of chapter 15.
Next, a couple of non-textbook problems:
- (12 pt)
The atmosphere of Mars is rather dilute — average surface pressure P=600 Pa,
less than 1% of the air pressure on Earth.
It constist mostly of carbon dioxide CO2
(molecular weight 44, adiabatic coefficient γ=1.3).
During a winter night, the temperature on Mars drops to 170 Kelvin —
about 153 degrees Fahrenheit below zero.
According to the universal gas law, the density of CO2 under such
conditions is ρ=18 g/m3 (note units).
Calculate the speed of sound on Mars.
- (15 pt) Consider two organ pipes:
The first pipe is open at both ends, while the second pipe
is open at one end and closed at the other.
Both pipes have the same length L=1.5 meter (about 5 feet).
(a) Find the wavelength of the lowest harmonic for each pipe.
(b) Find the wavelengths of the next two harmonics for each pipe.
(c) Find the frequencies of all those harmonics when the speed of sound
in the air is u=340 m/s.
Finally, questions Q2 (6 pt), Q4 (6 pt),
and problem SP1 (12pt) at the end of chapter 16.
Due October 15 (Wednesday); solutions.
Set 7
Textbook questions and problems Q10, SP2 (15 pt), Q23,
E10, E14, and Q28
at the end of chapter 16.
One non-textbook problem (15 pt):
- Surface of a crystal is covered by a thin layer of oil, just 450 nm (nanometers) thick.
Light shines on this surface and some of it is reflected back;
for simplicity, assume that both the incoming and the reflected light waves move
perpendiculary to the surface.
(a) Both sides of the oil layer reflect light, but the light waves reflected
by different sides travel through different distances.
Find the difference between the two distances.
(b) The oil has refraction coefficient n=1.488, which means the light
travels through it at reduced speed c/n
(cf. problem SP1 from the previous homework set).
Find the wavelengths in the oil of the red, green, and blue light waves
with respective frequencies 448, 560, and 672 TeraHertz.
(1 THz=1·1012 Hz.)
(c) For each of the three colors of light, compare its wavelength to the difference between
distances traveled by the two reflected waves, and find if the interference
between those two waves is constructive or destructive.
(d) Suppose the light shining on the oil-covered crystal is white.
What is the color of the reflected light?
Due October 22 (Wednesday); solutions.
Set 8
Six textbook questions and problems: Q8, Q26,
E4, Q16, Q17, and E7
at the end of chapter 17.
One non-textbook problem:
- (15 pt) A concave mirror has curvature radius R=30 cm.
(a) If a parallel beam of light (from a laser, or from a very distant lamp) shines on
this mirror, would the reflected rays converge or diverge?
Where would they cross or appear to cross?
(b) An object is placed 10 cm in front of the mirror.
Where is the image of this object: in front of the mirror or behind it, and at what distance?
Is this image real or virtual? Is it up-right or upside-down?
(c) Another object is placed 20 cm in front of the mirror.
Where is the image of the second object:
in front of the mirror or behind it, and at what distance?
Is this image real or virtual? Is it up-right or upside-down?
Due October 29; solutions.
Set 9
Textbook problem E16 at the end of chapter 17.
Non-textbook problems:
- (12 pt)
(a) If a person needs eyeglasses with negative lenses, is s/he near-sighted or far-sighted?
(b) If a person needs eyeglasses with positive lenses, is s/he near-sighted or far-sighted?
(c) Some people need positive lenses for reading but negative lenses for driving.
What can you say about their eyes? What's wrong with them?
(d) Could anybody need negative lenses for reading but positive lenses for driving?
Please explain your answer.
- (15 pt)
Consider a two-lens microscope.
The objective lens has focal distance 12.0 mm while the ocular (eyepiece) lens has focal distance 25.0 mm.
The object — an infusoria fixed to a glass slide — is held at distance 13.0 mm from the objective lens.
(a) Where is the image of this infusoria in the objective lens?
(b) What is the magnification of this image?
(c) Where would you put the ocular lens relative to this image so that its image would be 25 cm
in front the observer's eye (which is just behind the ocular)?
(d) How much further magnification do you get from the ocular?
(e) The infusoria is 0.2 mm long. How long is its image in the microscope?
- (6 pt)
In a chemical reaction, the net mass is conserved.
But when a piece of wood is burned, the remaining ash weights much less than the wood.
Please resolve this paradox.
- (6 pt)
Consider the chemical reachion 2H2+O2→2H2O
in which hydrogen combines with oxygen to make water.
(a) Do the numbers of hydrogen and oxygen atoms change in this reaction?
(b) What about the numbers of hydrogen and oxygen molecules? Do they change or stay the same?
Textbook problems E2 and E4
at the end of chapter 18.
Due November 7 (Friday); solutions.
Set 10
Textbook question Q21 at the end of chapter 18.
Non-textbook problems:
- Suppose you have a beam of particles flying along some tube, and you don't know what those particles are.
(a) How would you find whether the particles are electrically charged or neutral, and if charged,
is the charge positive or negative?
(b) How would you measure the charge-to mass ratio Q/M of the particles in the beam?
- As recently as 10 years ago, most TV sets and computer monitors were cathode ray tubes, in which
beams of electrons produce light when the strike the screen.
The X-ray tubes are also CRTs, in which fast electrons strike the anode and prodice X rays.
Did the CRT televisions and monitors produce X rays? Were they safe to watch?
Please explain your answer.
- (12 pt) Natural copper is a mixture of the two isotopes, about 69% of
6329Cu
and 31% of 6529Cu.
(a) Find the numbers of protons, neutrons, and electrons in a single neutral atom of each isotope.
(b) Find the atomic weight of a natural copper.
- (12 pt) An unstable nucleus has atom number Z and mass number A.
What would be the atom number and the mass number of a daugther nucleus
(a) in an α decay? (b) in a β decay? in a γ decay?
Textbook question Q5 (6pt) and problems E8
and SP2 (15pt) at the end of chapter 19.
Updated 11/12: Texbook problem E8 is postponed to the next homework set.
Due November 14 (Friday); solutions.
Set 11
Textbook problems E8, Q19, and E11
at the end of chapter 19.
Non-textbook problems:
- (12 pt) In 1952, the US tested the very first fusion device (Ivy Mike, not weaponized) and blew up
the Elugelab island.
The explosion energy was about 47·1015 J —
the equivalent of 11 megatons of TNT or 750 Hirosima bombs.
23% of that energy came from deuterium fusion; the rest came from secondary fission in the
uranium tamper.
The deuterium fusion reactions can be summarized as
3D → α + p + n
where D is a deuteron (deuterium 2H nucleus) of mass 2.014,102 amu,
α is an alpha particle (helium 4He nucleus) of mass 4.001,506 amu,
p is a free proton of mass 1.007,276 amu,
and n is a free neutron of mass 1.008,665 amu.
(a) When 3 deuterons participate in this reaction, how much mass is lost and converted to energy?
(b) How much energy do you get from this conversion?
For your information, 1 amu=1.6605·10-27 kg,
c=2.9979· 108 m/s.
(c) How much deuterium (in kilograms) was fused during the Ivy Mike test?
- (12 pt) An electron microscope uses beams of fast electrons instead of light to view very small objects.
Typically, the electrons are accelerated by a 100 kilovolt potential difference, made into a tight beam
aimed at the object, and then manipulated by sideways electric and magnetic fields that act like lenses
to form a magnified image on the screen.
(*) Each electron has mass m=9.11×10−31 kg
and charge q=−1.60×−19 C.
Once it's accelerated by a 100 kilovolt potential difference, it acquires
kinetic energy E=1.60×10−14 J,
velocity v=1.64×108 m/s,
and momentum p=1.79×10−22 kg·m/s.
(a) Find the de Broglie wavelength of such an electron.
(b) If an electromagnetic wave had such a wavelength, would it be microwave, infrared, visible light, ultraviolet,
X-ray, or gamma-ray?
(c) What would be the frequency of such EM wave?
(d) Find the energy of one photon of this wave and compare it to the electron's energy.
Textbook problems Q29 and SP2 (12pt).
at the end of chapter 18.
Due November 21 (Friday); solutions.
Set 12
Textbook questions Q8 (8pt), Q10
and problems SP2 (12 pt), E9 (8pt) , E10
at the end of chapter 20.
Non-textbook problems:
- (15pt) Consider 3 jet planes flying at similar airpeeds 570 MPH in a strong wind
blowing from West to East at speed 100 MPH.
(a) The first plane flies due East. Find its grounsdpeed.
(b) The second plane flies due West. Find its groundspeed.
(c) The third plane heads due North.
Find the direction of its flight relative to the ground.
(d) Find the groundspeed of the third plane.
Note on terminology: The airspeed of a plane is the magnitude of its velocity relative to the
moving air, while the groundspeed is the magnitude of its velocity relative to the ground.
The heading of the plane is the direction of its velocity relative to the air, while the
direction of the plane's velocity relative to the ground is called the flight direction.
- Consider an interstellar space probe — hopefully to be launched in a few decades —
moving from Earth to a planet of Tau Ceti at speed v=0.80 c
(80% of lightspeed).
The rest mass of the probe is 1200 kg.
Calculate the kinetic energy and the momentum of the probe using relativistic formulae.
Update 11/27: in textbook problem E9, change the spaceship's velocity to v=0.8 c
(80% of lightspeed).
Due December 5 (Friday); solutions.
Last Modified: December 6, 2014.
Vadim Kaplunovsky
vadim@physics.utexas.edu

