Homework for PHY 309K
Welcome to homework assignments for the Elementary Physics (I)
course, PHY 309 K.
The homeworks on this page are for the section taught by
Professor
Vadim Kaplunovsky in Spring 2014 (unique #58900).
Other sections assign different homeworks.
Many homework problems are taken from the Griffith and Brosing
textbook; such problems are listed by chapters and numbers,
for example Q2 at the end of chapter 3.
Please note the letter in the beginning of each number: Q2, E2, and SP2 are
different problems.
Also, the numbers are according to the 7th edition;
if you use an older or a newer edition, the number in your book will be different.
In addition to the textbook problems, I will make some problems of my own, or copy
problems from other books.
All such non-textbook problems will be written down on this page.
For grading purposes, the harder problems will be worth more points than the easier problems.
The pointage will be shown after each problem;
if the pointage is not shown, the problem is worth 10 points.
Please note that the physical laws and the formulae you use
and the way you put them together are more important for your grade
than the numbers you calculate.
If you understand the physics governing a problem, use correct formulae,
and properly put them together, you would get a high partial score even
if your arithmetic is faulty.
But you would get a low score for a numerical answer without a clear explanation of
where it came from, even if the number happens to be correct.
Schedule of Homeworks and Exams.
Note: The textbook chapters in the schedule are tentative.
They may change if the class goes faster or slower than I expect.
| Set | Assigned | Due | Chapter(s) |
|---|
| Set 1 | January 14 | January 21 (Tuesday) |
1, 2 |
| Set 2 | January 21 | January 28 (Tuesday) |
2, 3 |
| Set 3 | January 28 | February 4 (Tuesday) |
3 |
| Set 4 | February 4 | February 11 (Tuesday) |
3, vectors, §20.1 |
| Midterm 1 | February 13 (Thursday) |
1, 2, 3, vectors, §20.1, §4.1–2 |
| Set 5 | February 13 | February 20 (Thursday) |
§20.1, 4 |
| Set 6 | February 20 | February 27 (Thursday) |
friction, 5 |
| Set 7 | February 27 | March 6 (Thursday) |
5, 6 |
| Set 8 | March 6 | March 20 (Thursday) |
6, 7 |
| Midterm 2 | March 25 (Tuesday) |
4, friction, 5, 6, 7 |
| Set 9 | March 25 | April 1 (Tuesday) |
7, 8 |
| Set 10 | April 1 | April 8 (Tuesday) |
8 |
| Set 11 | April 8 | April 15 (Tuesday) |
8, 9 |
| Set 12 | April 15 | April 22 (Tuesday) |
9 |
| Midterm 3 | April 24 (Thursday) |
7, 8, 9, 10 |
| Set 13 | April 24 | May 1 (Thursday) |
10 |
| Final Exam | May 7 (Wednesday), 2–5 PM |
everything |
Each homework set should be posted by the "assigned" date in this schedule.
If it is not, let me know ASAP.
Exams
Homework sets
Set 1
Only non-textbook problems this time:
- Enrico Fermi once gave a class which lasted precisely 1 microcentury.
How long was his class in minutes?
- A British naturalist with a penchant for archaic units once reported the
average speed of a snail as 1 furlong per fortnight.
(A furlong is one eighth of a mile or 220 yards; a fortnight is 14 days and nights.)
How far would a snail crawl in one minute?
Please state your answer in metric units.
- How many liters of paint does it take to paint two yellow lines
in the middle of a 100 kilometer long highway?
For the sake of definiteness, assume each line is 10 cm wide and 1 mm thick.
(Or rather, when the yellow paint was still wet, it was 1 mm thick.)
- (12 pt) Several solid balls of different sizes are made from the same material.
(a) Show that the mass of a ball is proportional to the cube of its radius,
M∝R3.
(b) The second ball has twice the radius of the first ball,
R2=2R1.
The first ball has mass M1=1 kg;
what is the mass M2 of the second ball?
- Your friend is celebrating his 20th birthday. What is his age in seconds?
Please write your answer with a correct number of significant figures.
Note that you do not know the hour — let alone the second — of his birth, only the day.
- A student weighs 150 lb, his backpack 17.3 lb.
Write down their combined weight with a correct number of significant figures.
Due January 21; solutions.
Set 2
First, three easy textbook questions from the end of chapter 2:
Q4, Q22, Q23.
Second, a non-textbook problem:
- (12 pt) A driver wishing to go from Austin to San Antonio (80 miles South of Austin)
takes a wrong ramp into I-35 and ends up going North instead of South.
He does not notice his mistake until he gets to Waco (100 miles North of Austin).
At that point he turns around, goes back to Austin and continues on to San Antonio.
The whole trip took 4 hours.
For this trip, find:
(a) the net displacement;
(b) the total distance travelled;
(c) the average velocity;
(d) the average speed.
Third, two more textbook problems from the end of chapter 2:
E14, E16.
Finally, another non-textbook problem:
- (15 pt) A rock laying on a roof of a 144-feet-high building is dislodged and falls
down with zero initial velocity.
For simplicity, neglect the air resistance and approximate the free-fall acceleration as
g≈32 ft/s2.
(a) How long does the rock stays in motion before it hits the ground?
(b) What is the speed of the rock when it hits the ground?
(c) Convert this speed into meters/second, kilometers/hour, and miles/hour.
Due January 28 January 30; solutions.
Set 3
Because of the canceled class on 1/28, this homework is rather short: 5 problems about free fall only.
The vector problems I wanted to include with this homework are postponed to set 4.
First, two easy textbook questions from the end of chapter 3:
Q14, Q17.
Second, 3 non-textbook problems about free fall.
In problems I and II, neglect air resistance and approximate g=10 m/s2.
- (12 pt) A ball is kicked vertically up from the ground with initial velocity 15 m/s.
(a) How much time does it take the ball to reach its maximal height?
(b) What is the maximal height reached by the ball?
(c) How long does it take the ball to fall back to the ground?
(d) What is the ball's velocity when it hits the ground?
- (15 pt) Joe Blow stands on a balcony 25 meters (80 feet) above the ground.
He throws two empty bottles, the first with initial velocity 20 m/s (45 MPH)
vertically down, and the second with initial velocity 20 m/s vertically up.
(a) How much time does it take the first bottle to reach the ground?
(b) With what velocity does it hit the ground?
(c) The second bottle starts going up, reaches maximal height, falls down,
barely misses Joe's head on its way down, and eventually hits the ground.
What much time does its whole flight take?
(d) With what velocity does the second bottle hit the ground?
(e) Verify the formula
v2−v02=
2g×(x0-x)
for each bottle.
Warning: Please don't throw bottles from a balcony, you might hurt somebody.
- An astronaut on the Moon tossed a rock up; 22 seconds later, the rock fell back on the ground.
What was the maximal height reached by the rock during its flight?
Note: Lunar gravity is much weaker than Earth's, so the free-fall acceleration on the Moon is only
gM=1.6 m/s2.
Hint: the rock was moving up for the first 11 seconds of its flight, then falling down for another 11 seconds.
Due February 4; solutions.
Set 4
Only non-textbook problems this time: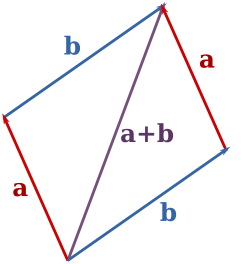
- The figure on the right shows two vectors a and b and their sum a+b.
Draw similar pictures for the a−b, b−a, and a−2b.
- A yacht sails for 6.0 hours with constant velocity vector 10.0 knots (nautical miles per hour) directed
South–SouthWest (202.5° clockwise from North).
Find the southward and the westward displacement of the yacht during this time.
For simplicity, answer in units of nautical miles.
- (12 pt) A plane flies due North for 93 miles, then turns and flies 186 miles in the direction 120°
(clockwise from North), and then turns again and flies another 93 miles in the direction 210°
(clockwise from North).
(a) Draw a map of the plane's motion.
(b) Find the net displacement of the plane in (N,E) components.
(c) Find the magnitude and the direction of the net displacement vector.
- (12 pt) A small airplane delivers emergency supplies to a team of geologists stuck at a remote location.
The pilot does not find a place to land, so he simply drops the bag with the supplies
while flying 180 meters (600 feet) directly above the geologist's camp.
The bag falls down as a projectile with initial velocity vector equal to the plane's velocity,
namely v0x=45 m/s (about 100 MPH), v0y=0.
(a) How long does it take the supply bag to fall to the ground?
(b) How far from the camp does it land?
(c) What is the velocity vector of the bag when it hits the ground?
(d) Convert the x and y components of this vector into magnitude and direction.
- (12 pt) Two water jets in a fountain emerge from almost the same point at the ground level.
One jet follows a low trajectory, the other follows a high trajectory, but both jets hit
the ground at the same point, 5 meters from the starting point of the jets.
(a) The first jet starts with initial angle θ1=15° above the ground.
What is the initial speed v0 of water in this jet?
(b) The second jet has the same initial speed of water but higher initial angle
θ2>θ1. Find that angle θ2.
- A riverboat steams back and forth between two cities 30 miles apart.
The river's current has speed 5 MPH,
the boat's speed relative to the water is 15 MPH.
(a) How much time does the boat take to steam 30 miles upstream?
(b) How much time does it take to steam back (the same 30 miles, but downstream)?
(15pt) A small plane flies at airspeed 120 MPH from Austin to Oklahoma City,
360 miles due North from Austin.
The wind blows at speed 60 MPH in the direction from West to East.
(a) If the pilot does not know about the wind and the plane is heading due
North, what is its direction of flight relative to the ground?
(b) By the time the plane reaches the latitude of the Oklahoma City, how far
East off the target would it be?
(c) If the pilot does now about the wind velocity, in what direction should he head
the plane in order to make it to the Oklahoma City?
(d) How much time would this flight take?
Note on terminology: The airspeed of a plane is the magnitude of its velocity relative to the
moving air, while the groundspeed is the magnitude of its velocity relative to the ground.
The heading of the plane is the direction of its velocity relative to the air, while the
direction of the plane's velocity relative to the ground is called the flight direction.
Updated 2/6 at 7 PM: Problem VII is postponed to the next homework.
Due February 11; solutions.
Set 5
First, 4 non-textbook problems:
(15pt)(5pt) A small plane flies at airspeed 120 MPH from Austin to Oklahoma City,
360 miles due North from Austin.
The wind blows at speed 60 MPH in the direction from West to East.
(a) If the pilot does not know about the wind and the plane is heading due
North, what is its direction of flight relative to the ground?
(b) By the time the plane reaches the latitude of the Oklahoma City, how far
East off the target would it be?
(c) If the pilot does now about the wind velocity, in what direction should he head
the plane in order to make it to the Oklahoma City?
(d) How much time would this flight take?
Note on terminology: The airspeed of a plane is the magnitude of its velocity relative to the
moving air, while the groundspeed is the magnitude of its velocity relative to the ground.
The heading of the plane is the direction of its velocity relative to the air, while the
direction of the plane's velocity relative to the ground is called the flight direction.
- Next time you ride a bus (or a car) and your bag is laying on the empty seat next to you,
note what happens when the bus suddenly slows down:
The bag slides off the seat, flies forward, and hits the back of the seat in front of it.
There are no horizontal forces acting on the bag, so why does not it stay at rest?
Explain this behavior in terms of the Newton's First Law.
- Mars has a weaker gravitational field then Earth, g(Mars)=3.7 m/s2.
How much would you weigh on Mars compared to your weight on Earth?
- John and Mary stand on very slippery ice at some distance from each other holding two ends of a rope.
John's mass is 77 kg (including the clothes), Mary's mass is 55 kg (also including the clothes); rope's mass is too small to matter.
When John and Mary pull on the rope, John accelerates towards Mary at aJ=2.5 m/s2.
What is Mary's acceleration?
Second, textbook question Q29 and problems SP6 (12 pt) and SP5 (12 pt)
from the end of chapter 4.
Update 2/17 at 11 PM: Since the posted solutions to homework set#4 include the non-textbook problem I of this set,
its pointage is reduced to 5pt only. To get those 5 points, you should explain the solution in your own words.
Due February 20; solutions.
Set 6
First, several non-textbook problems:
- Suppose you need to move a 68 kg (150 pounds) box along a rough horizontal floor.
You push the box with increasing force F, until the box begins to move
for F=330 N (74 pounds).
When you continue to push the box with the same 330 N force, it accelerates
forward with a=1.0 m/s2.
Find the coefficients of static and kinetic friction between the box and the floor.
- Consider a 800 kg car with good breaks but bad tires moving on a wet (but not water-covered)
road at speed 50 MPH (22 m/s).
Under this conditions, the static friction coefficeient between the tires and the
pavement is μs=0.40 while the
kinetic friction coefficient is μk=0.30.
Find the shortest possible stopping distance of this car (a) without skidding and (b)
while skidding all the way to the stop.
- A parachute has air-drag coefficient D=52 kg/m.
What would be the terminal velocity of a 85 kg (188 lb) man jumping with this parachute?
- As the Earth spins, every point on its surface moves in a latitude circle once every 24 hours.
In particular, Austin moves in a circle of radius 5500 km, while Anchorage (Alaska) moves
in a smaller circle of radius 3100 km.
(a) Find the speed of each city relative to the Earth's center.
Hint: length of a circle=2πR.
(b) Find the centripetal acceleration of each city.
(c) The centripetal acceleration is inversely proportional to the radius of the circle.
However, Austin which moves in a larger circle than Ancorage nevertheless
has a larger centripetal acceleration.
Explain this seeming paradox.
- A road goes over the top of a hill along an arc of a vertical circle of radius 95 m.
A 800 kg car moves along this road at speed 22 m/s (50 MPH).
(a) Find the centripetal acceleration of the car.
(b) Find the normal force from the road on the car when the car is at the top of the hill.
(c) What would happen to another car going over the same hill but at higher speed
33 m/s (75 MPH)?
- Another road has a flat (un-banked) curve of radius 30 m (100 feet).
If the tires of your car have static friction coefficient μs=0.60,
what is the highest speed at which your car can negotiate this curve?
- A train moves at increasing speed along gently curving horizontal tracks
(radius of curvature R=1200 m, about 3/4 of a mile).
For simplicity, assume the train's speed increases at uniform rate from
20 m/s (45 MPH) to 40 m/s (90 MPH) in 20 seconds.
(a) Find the tangential acceleration of the train.
(b) Find the normal (centripetal) acceleration of the train at the time its speed
is 30 m/s (67 MPH).
(c) Find the net horizontal force acting on a 60,000 kg train car at that moment.
PS: assume all numbers to be accurate to 2 significant figures.
Finally, textbook problem SP2 from the end of chapter 5.
Due February 27; solutions.
Set 7
First, an easy textbook question: Q25 from the end of chapter 5.
Second, 3 non-textbook problems:
- Distances between planets are often measured in astronomical units
(au) where 1 au = 149.6×106 km
is the average radius (semi-major axis) of the Earth's orbit around the Sun.
Planet Mercury has an elliptic orbit of average radius (semi-major axis)
0.387 au and eccentricity approximately 20% (i.e., ε=0.20).
(a) How close does Mercury get to the Sun at the closest point of its orbit (the perihelion)?
(b) How far is it from the Sun at its most distant point (the aphelion)?
(c) How long is Mercurian year (i.e., the orbital period of Mercury)?
- In 2005 the
Huygens
probe landed on the Saturn's moon Titan and reported a surprisingly Earth-like
world: dense atmosphere, seas, rivers, etc. Titan is bigger than Luna but smaller than
Earth, and less dense. To be precise, its radius is 0.404 of R_Earth but its mass is only
0.0225 M_Earth.
If you go to Titan, how much would you weigh there compared to your weight on Earth?
- Titan's orbit around Saturn has semi-major axis a=1.222·109 m
(759,000 miles) and period T=1377600 s (15.945 days).
Use these data to find the mass of Saturn.
Third, another easy textbook question: Q2 from the end of chapter 6.
Finally, another 3 non-textbook problems: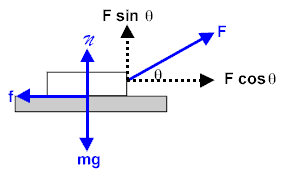
- A rope pulls heavy box along the floor; the forces acting on the box are shown on the diagram to the right.
Consider the mechanical work done by each of these forces.
Which force(s) do positive work? Which force(s) do negative work? And which force(s) do zero work?
Please explain your answers.
- A man pulls a 10.0 kg bucket full of water out of a deep well.
Man's mechanical work is 5900 J. How deep is the well?
- A big horse working hard has mechanical power of about one horsepower,
hence the name of the unit.
In English units 1 hp = 550 feet-pounds per second, and in metric 1 hp = 746 W.
Consider a horse pulling a 160 kg (350 lb) sleigh on a horizontal snowed-over ground.
The kinetic friction coefficient between the snow and the sleight is 0.12.
(a) With what force should the horse pull the sleigh to keep it moving at constant speed?
(b) With what maximal speed can the horse pull the sleigh if his power is limited to 1 hp?
Due March 6; solutions.
Set 8
Only non-textbook problems this time:
- How fast should a 57 g tennis ball move in order to have the same
kinetic energy as a 7.0 kg bowling ball moving at 5.0 m/s?
- A 9.0 g bullet hits a tree with impact speed of 250 m/s.
The bullet makes a 8.0 cm long hole in the wood, then stops.
Find the average force resisting the bullet's motion through the wood.
- A 1200 kg car is parked on a very steep downhill road (20° below horizontal),
which turns out to be a bad idea:
After a sudden rain, the friction force between the tires and the road became
too small to keep the car from sliding down.
Once the car started sliding, the kinetic friction force between the tires and the wet road
was only 2500 N.
(a) List all the forces acting on the car and calculate the work of each force
while the car was sliding 120 meters (400 feet) down the road.
(b) Find the speed of the car at the end of this 120 m slide.
- When the Lake Mead above the Hoover Dam is full, the water in the lake is 180 m (600 feet) above
the water below the dam.
Suppose the water flows through the power station turbines at the rate of 1100 m3/s.
(a) How much potential energy of water is released every second?
(b) If 90% of that energy is converted to electricity, what is the electric power produced by
the Hoover Dam?
- (15 pt) A 2.0 kg steel ball suspended on a 3.0 meter long cable swings back and forth like a pendulum.
When the ball reaches an end of a swing and turns back, the cable's direction is 45° from the vertical.
(a) Find the height of the ball's turning points (there are 2 of them) relative to the lowest point
of the ball's trajectory.
(b) Find the speed of the ball when it goes through the lowest point.
(c) Find the tension of the cable when the ball goes through the lowest point.
(d) Find the speed of the ball when the cable makes angle 30° with the vertical.
- (15 pt) In a bungee jump
(illustration)
the cord acts like a spring when stretched: its tension T depends
on length L as T=k(L-L0)
for some force constant k and un-stretched length L0.
However, for L<L0 the cord folds instead of
becoming compressed, so there is no tension force and no elastic energy.
Consider a bunjee cord of un-stretched length 21 meters (70 feet).
To test its reliability, one end of the cord is tied to a steel ball of mass 122 kg (270 lb)
while the other end is tied to a bridge, 61 m (200 feet) above the water.
The ball is dropped off the bridge (with zero initial velocity) and falls down;
but once the cord becomes stretched, its tension slows down the fall;
eventually, it stops the ball and then yanks it back up.
The lowest point reached by the ball is 1 m above the water, 60 m below the bridge.
(a) Describe what happens to the kinetic and the potential energy of the ball
and the elastic energy of the cord while the ball falls down.
(b) Find the force constant k of the cord.
(c) Find the speed of the ball at the moment it was 11 meters above the water.
- A 56 gram tennis ball hits a wall and bounces off.
Before the collision, the ball had velocity components
(vx=+38 m/s, vy=+2 m/s);
after the collision, its velocity components were
(vx=-32 m/s, vy=+2 m/s).
Note change of direction!
(a) What was the change of the ball's momentum vector during its collision with the wall?
(b) If the collision lasted for 3.5·10-3 s, what was the
average force on the ball during this time?
Smith & Wesson 44 Magnum revolver shoots a 13 g bullet at very high speed
495 m/s (1625 ft/s or 1106 MPH).
The gun itself has mass 1400 g (3.1 lb).
People who shoot this gun must hold it very tightly to control its recoil.
If some fool holds it loosely in his hand, what would be the recoil speed of the gun?
Update 3/18: Problem VIII is canceled.
Due March 20 (Thursday after the Spring break); solutions.
Set 9
First, four non-textbook problems about collisions and rockets;
for problems II and III on elastic collisions, see formulae on pages 4–6 of
my notes on collisions.
- (15 pt) A 4400 kg (9600 lb) truck is southbound on the Guadalupe street.
When it enters the intersection with the MLK boulevard, its velocity is 11 m/s (24 MPH)
in the direction 30° East from South. (Note that the Guadalupe street bends at the intersection.)
A 1100 kg (2400 lb) car going West on the MLK runs a red light and collides with the truck.
The two vehicles become stuck together in the collision, and the combined wreckage moves
due South until it hits the 7/11 gas station at the corner.
(a) What was the Eastward component of the truck's momentum before the collision?
(b) What was the Eastward component of two vehicules' net momentum after the collision?
(c) What was the Westward momentum of the car before the collision?
(d) How fast was the car moving when it hit the truck?
- In a nuclear physics lab, a heluim nucleus (an alpha particle) collides head-on with an oxygen
nucleus and bounces back.
The oxygen nucleus is 4 times heavier than the helium nucleus,
MO=4.00×MHe.
Before the collision, the oxygen nucleus is at rest while the helium nucleus moves with velocity
15.0·106 m/s.
Find the velocities of the two nuclei after the collision.
- (15 pt) In class I demonstrated a double-ball drop: A tennis ball is put on top of a basketball,
and both balls are dropped down at almost the same time. The basketball hits the floor
and bounces up, then collides with the tennis ball falling down.
The basketball is 10 times heavier than the tennis ball, Mbasketball=570 g
while Mtennis ball=57 g.
Assume both collisions — of the basketball with the floor, and of the tennis ball with the
basketball — are perfectly elastic and head-on, and neglect the air drag and other resistive forces.
(a) The two balls are dropped from height 1.2 meters (4 feet) above the floor.
What are their velocities just before the basketball hits the floor?
(b) What are the two balls' velocities after the basketball bounces up but before it hits the tennis ball?
(c) What are their velocities after they hit each other?
(d) How high will each ball rise in the air after their collision?
- A space shuttle had three main rocket engines and two solid-rocket boosters.
At maximal power, each main engine burned 55 kg of liquid hydrogen and 440 kg of liguid oxygen
every second; the exhaust H2O gas jetted out at speed 4440 m/s.
Each booster burned 5200 kg of solid fuel+oxydizer mix (mostly aluminum, polybutadiene polymer,
and ammonium perchlorate) every second; the burn products jetted out at speed 2630 m/s.
(a) Find the thrust force of each rocket engine.
(b) At liftoff, the shuttle assembly (the orbiter, the external fuel tank, and the two boosters)
had mass 2.03·106 kg.
If all the engines had their maximal thrust at liftoff, what would be the shuttle's
acceleration?
Second, three textbook problems about the torque: E8, E10,
and SP2 at the end of chapter 8.
Due April 1; solutions.
Set 10
Only non-textbook problems this time: 
- Picture at the right shows a drawbridge at the gate of a medieval castle.
The bridge is 3.3 meters (11 feet) long and weighs 3200 N (720 pounds); its center of gravity is in the middle of the bridge.
The castle end of the bridge is pivoted on a well-greased axle, while two lifting chains are attached to the
other end of the bridge.
When the bridge is horizontal, the chains make angle θ=40° with the bridge.
Find the net tension of the two chains required to lift the bridge (or at least to begin lifting it).
- Two paramedics, Bob and Charlie, carry a 200 lb patient on an 8-foot-long stretcher.
Bob holds the front end of the stretcher and Charlie holds the back end.
The patient lies closer to the front end of the stretcher, so his center of gravity is 3 feet from Bob's hands
and 5 feet from Charlie's. How much of the patient's weight is carried by Bob and how much by Charlie?
- Joe Blow put an abstract sculpure in his yard: A cylindrical column made of solid concrete,
standing vertically on a horizontal platform, also made of concrete.
The column's height is 12 feet and its diameter is 6 inches.
(a) Where is the center of gravity of the column?
(b) After heavy rains, the ground below the platform became soft, and the platform started tilting, which made the
column lean away from vertical by a small angle θ=1.0°.
Find the horizontal displacement of the column's center of gravity relative to the center of the column's bottom end.
(c) The column's angle θ from the vertical was slowly increasing over the next few days, and eventually
the column lost stability and toppled to the ground.
What was the lean angle θ when the column lost stability?
- Another abstract sculpture consists of a hollow bronze sphere on top of a
vertical cylinder made from solid aluminum.
The sphere has outer radius 0.50 m, uniform thickness 5.7 mm, and mass 160 kg.
The cylinder has radius 0.20 m, height 1.00 m, and mass 340 kg.
(a) Where is the cylinder's center of mass?
(b) Where is the sphere's center of mass? What is its height above the floor
(on which the cylinder stands)?
(c) How high is the center of mass of the whole sculpture?
- (12 pt) To test the balance of a bicycle wheel, it is removed from the bike and spun to a high rotation
rate of 3000 RPM.
(a) What is the angular velocity of this wheel in rad/s?
(b) The nipple of the tire is located 28 cm from the wheel's axis.
Find the linear speed and the centripetal acceleration of the nipple.
(c) After the test, a wet rag was pressed agains the tire, and the torque of the
friction force made the wheel stop in 30 seconds.
What was the angular acceleration of the wheel during this time?
(d) How many revolutions did the wheel make while slowing down?
- (12 pt) A grinding wheel is a disk of uniform density and thickness.
It has mass M=2.4 kg and radius R=40 cm.
(a) Find the moment of inertia of the wheel.
(b) The wheel is rotating at the rate of 720 RPM. Find its kinetic energy.
(c) Find the angular momenum of the wheel.
(d) Once the motor is turned off, the friction stops the wheel in 40 seconds.
Find the torque of the friction forces.
- (15 pt) A rod has mass M=1.20 kg, length L=1.00 m, and uniform density and thickness.
The rod is swinging on a frictionless pivot attached to rod's end; the other end of the rod is free.
The rod is held at angle θ=30° above the horizontal, then released with no initial
angular velocity, ω0=0.
(a) What is the moment of inertia of the swinging rod?
(b) What was the torque of the gravity force on the rod when the rod was released?
(c) What was the angular acceleration of the rod when it was released?
(d) What was the linear acceleration of the rod's free end at the moment of release?
(e) For extra 5 points, write an algebraic formula for the linear acceleration of the free end
and show that it does not depend on the rod's mass or length.
Due April 8; solutions.
Set 11
First, three textbook problems at the end of chapter 8: E18,
SP3 (12 pt) and SP4 (12 pt).
In problem SP4, change the wheel's moment of intertia from
I=2 kg·m2 to a more realistic value I=0.060 kg·m2.
Next, two non-textbook problems: 
- The picture on the right shows a bicycle wheel «gyroscope» similar to the one I demonstrated in class.
The wheel is spinning rapidly on its axis, while the axis itself slowly turns right or left due to presession.
(a) At the moment the picture was taken, the wheel is spinning clockwise (from the camera's point of view).
What is the direction of the wheel's angular momentum vector?
(b) The upward force of the string tied to the wheel's axis is misaligned with the wheel's weight, which
makes for a non-zero net torque. What is the direction of this torque vector?
(c) Which way is the wheel's axis precessing, left or right?
- The Challenger Deep (named after research ship Challenger II)
is the deepest place in all the oceans of Earth; it's 10923 meters (35840 feet, or almost 7 miles)
below the surface.
What is the water pressure at the bottom of the Challenger deep?
Note that seawater is a bit denser than fresh water;
for the purpose of this exercise, use ρ(seawater)=1050 kg/m3.
Finally, three textbook problems at the end of chapter 9:
Q5. Q10, and E5.
Due April 15; solutions.
Set 12
Only non-textbook problems this time:
- The deepest lake in the US is Crater Lake in Oregon:
its maximal depth is 594 m (almost 200 feet).
The surface of the lake is at altitude 1883 m (6178 feet) where the air pressure averages 81 kPa.
A small gas bubble of volume 1.0 mm3 forms at the bottom of the lake (in the deepest part)
and slowly rises to the lake's surface.
What would be the volume of this gas bubble just before it bursts at the surface?
For simplicity, assume the temperature of the gas in the bubble remains constant at all times.
- A hot air balloon has volume 1800 m3.
The 240°F air inside the balloon has density ρin=0.91 kg/m3 while
the 80°F air outside the balloon has density ρout=1.18 kg/m3.
How much gross weight can this balloon lift to the sky?
The gross weight here includes the balloon itself, the gondola, and everything inside it,
but not the weight of the hot air inside the balloon.
- A glass bowl weighs 5.0 pounds in air, but when weighed underwater, its apparent weight is only
3.0 pounds. What is the density of glass this bowl is made of?
- An ice cube floats in a glass of warm water.
What happens to the water level when the ice melts?
Does it go up, down, or stays the same?
Please explain your answer.
- (12 pt) A horizontal water pipe of inner diameter 2.0 cm carries water at speed 11 m/s.
At some point, the pipe narrows down to 1.0 cm in diameter, and then the pipe ends and the water jets out.
(a) What is the speed of water in the narrow part of the pipe?
(b) The narrow part of the pipe opens to the air, so the water pressure there
is equal to the atmospheric pressure Patm=101 kPa.
What is the water pressure in the wide part of the pipe?
- (12 pt) An airplane flies at altitude where the atmospheric pressure is 78 kPa
and the air density is 1.00 kg/m3.
The plane has speed 63 m/s (140 MPH) relative to the un-disturbed air,
but the tilt of the plane's wings speeds up the airflow above the wings while slowing down the
airflow below the wings.
Relative to the plane, the air just above the wings moves at 67 m/s while
the air just below the wings moves at 55 m/s.
(a) What is the air pressure just above the plane's wings?
(b) What is the air pressure just below the plane's wings?
(c) The two wings of the plane have combined area 16 m2.
What is the lift force on the plane?
Note: To avoid round-off errors in part (c), keep extra figures in parts (a) and (b).
- This video
shows a beautiful curve-ball goal in a 1978 Brazil-Italy soccer game.
The ball starts parallel to the endline, but then veers right and flies into the goal,
right through a crowd of defenders who can't figure out where it's going.
Which way should the soccer ball spin to veer right?
How does one kick a ball to give it such spin?
Due April 22; solutions.
Set 13
Only non-textbook problems this time:
- Figure at the right shows an alcohol thermometer consisting of a thin vertical
cylinder connected to a much wider bulb at the bottom; the Fahrenheit and Celsius scales
are printed on a plate behind the cylinder.
The alcohol (dyed red) fills the bulb and the lower part of the cylinder.
The cylinder has internal cross-section A=0.25 mm2.
When the temperature increases, the alcohol level in the cylinder raises
by 1.00 mm for every degree Celsius of the temperature change.
Find the volume of the alcohol in the bulb below the cylinder.
The volume expansion coefficient of alcohol is β=1.12·10-3/°C.
For simplicity, neglect the thermal expansion of the glass containing the alcohol.
- Planet Venus has a thick atmosphere whose main constituent is
carbon dioxide (CO2) of molecular weight μ=44.
That is, 1 mol of CO2 has mass 44 grams.
Near the surface, the atmospheric pressure on Venus reaches 91 atm
(9.2 MPa) and the temperature 872°F (740 Kelvin).
Find the volume of 1 mol of CO2 under such conditions and hence the density of Venus atmosphere.
FYI, the universal gas constant is R=8.314 J/mol/K.
- Steinbier
is an ancient beer-making technology which involves heating wort in
wooden pots by dropping hot rocks into the pot.
Granite rock has specific heat cr=0.19 cal/g/°C
while wort has specific heat cw=1.04 cal/g/°C
(similar to water).
Suppose you drop 20 kg (44 pounds) of rocks heated to 360°C (680°F)
into 20 kg of 35°C (95°F) wort.
When the rocks and the wort reach thermal equilibrium, what would be their temperature?
- (12 pt) An experimental gun shoots big bullets made of ice at high speed.
When such a bullet (initially at -20°C) hits a target, its kinetic energy is converted
to heat, which warms the ice and melts some of it.
(a) If a 100 g bullet impacts the target at speed 400 m/s, how much ice would melt?
(b) At much higher impact speeds, there is enough energy to melt the whole bullet, heat the
resulting water to 100°C, and vaporise it all.
What is the minimal impact speed that would get the whole bullet vaporized?
For your information, liquid water has specific heat cwater=4.187 J/g/°C,
but the ice has smaller specific heat cice=2.108 J/g/°C,
the latent heat of melting ice is Lm=334 J/g,
and the latent heat of vaporizing water is Lv=2257 J/g.
- Human muscles have energy efficiency about 25%.
That is, out of every calorie of food energy used up by the muscles, only 1/4 calorie
is converted to mechanical energy while the remaining 3/4 calorie become heat.
During hard exercise, the body looses that heat by sweating:
The latent heat of evaporating sweat — 580 cal/g at body temperature —
uses up the extra heat produced by the hard-working muscles.
(a) Riding a bike at 20 mph speed on flat ground takes about 175 Watt of mechanical power.
If you ride at that speed for one hour, how many calories would you burn?
(b) How much sweat would evaporate off your body to dissipate the extra heat produced by your muscles?
Note that the food calories are actually kilocalories, 1 kcal=1000 cal=4187 J.
- For extra credit (15pt):
One mol of air (mass=29 g) has internal energy U=5⁄2RT
where R=8.134 J/K/mol is the universal gas constant.
Suppose you heat one mol of air from 300 K (80°F) to 500 K (440°F) while
keeping it at constant pressure P=100 kPa (but the volume increases).
(a) How much mechanical work is done by the expanding air?
(b) What is the change of the air's internal energy?
(c) How much heat does it take to heat the air?
(d) Suppose the same one mol of air was held at a constant but different pressure,
say P=200 kPa.
Would the amount of heat needed to change the air's temperature
from 300 K to 500 K the same as in part (c) of different?
(e) Now let's hold the air at constant volume V=25 L while the pressure increases
with temperature.
How much heat would it take to increase the air's temperature from 300 K to 500 K?
(f) If the air is held at a constant but different volume, say V=10 L, how would it
affect the amount of heat needed to change its temperature?
Would it be the same as in part (e) or different?
(g) Find the heat capacities Cp and Cv of one mol of air.
Update 4/29: Since I have not explained in class the material on which problem VI is based, I make it optional:
you do not have to solve it, but you can do it for extra credit.
Due on May 1; solutions.
Last Modified: May 7, 2014.
Vadim Kaplunovsky
vadim@physics.utexas.edu





