Homeworks for PHY 352 K
CLASSICAL ELECTRODYNAMICS (I)
Welcome to the homework assignment page for Classical Electrosynamics (I)
course (PHY 352 K) taught by
Professor
Vadim Kaplunovsky in Spring 2024 (unique number 56055).
Most homework problems are taken from the Griffith's textbook Introduction to Electrodynamics;
such problems are listed by their numbers in the textbook (page number in parentheses) according to the 4th
edition.
Note: if you have an older edition of the textbook, the problem numbers would be different!
If a homework set has any non-textbook problems, I shall either type it full at the appropriate place on this page,
or else give a link to a separate TeX–generated PDF file.
By default, each problem is worth 10 points.
But some problems may be worth more or fewer points; in that case I shall write down the pointage in brackets
right after the problem number.
Once a homework is collected, I post the solutions in TeX–generated PDF format.
The solutions will be linked to this page at the appropriate place.
Note: if for any reason you cannot come to the class on the day a homework is due, then
scan your homework (or take a clear picture with a digital camera or cellphone) and email it to me and to the TA.
Please don't waste time asking for my permission, just scan your work and email it, and make sure to do it
before the end of the class on which the homework is due.
Homework Sets
Set 1
Reading assignments: textbook sections §1.1 and §1.4.
Textbook problems from chapter 2:
2.2 (page 62), 2.3 (page 65), 2.5 (page 65), 2.6 (page 65).
Textbook problems from chapter 1:
1.6 (page 8), 1.11 (page 15), 1.13 (page 15).
No non-textbook problems in this set.
For the students who have not got their textbooks yet, here is
my transcription of the 7 homework problems.
Due January 25 (Thursday); solutions.
Set 2
Textbook problems from chapter 2 on applications of the Gauss Law:
2.15 (page 76), 2.16 (page 76), 2.18 (page 76).
Textbook problems from chapter 1 on vector calculus:
1.15 (page 18), 1.18 (page 20), 1.20 (page 20), 1.26 (page 24),
1.61 (page 56) [15 points], 1.62 (page 57) [15 points].
Textbook problems from chapter 2 on the electric potential:
2.20 (page 80), 2.21 (page 83), 2.22 (page 83).
No non-textbook problems in this set.
Due February 1 (Thursday); solutions.
Set 3
Textbook problems from chapter 1:
1.46 (page 49–50), 1.48 (page 52), 1.49 (page 52).
Textbook problems from chapter 2:
2.48 (page 108), 2.59 (page 112), 2.38 (page 102), 2.39 (page 102–103),
2.42 (page 104), 2.53 (page 109) [20 points].
No non-textbook problems in this set.
Due February 8 (Thursday); solutions.
Set 4
Textbook problems from chapter 2:
2.34 (page 95) [15 points], 2.35 (page 96), 2.37 (page 97) [15 points],
2.60 (page 112), 2.43 (page 107),
Notes for problem 2.60: (a) mind the induced charges;
(b) in some printings,
the textbook answer is a typo.
Non-textbook problem:
A circuit made from several capacitors connected to each other in some fashion
can be described by its equivalent capacitance — the ratio of the charge Q which would
flow through the outside wires when the whole circuit is allowed to discharge to the voltage V
between the outside wires.
(a) As a warm out exercise, derive the formulae for effective capacitance
of the series and parallel circuits of two capacitors C1 and C2.
(b) Now find the effective capacitance of the following infinite ladder circuit:
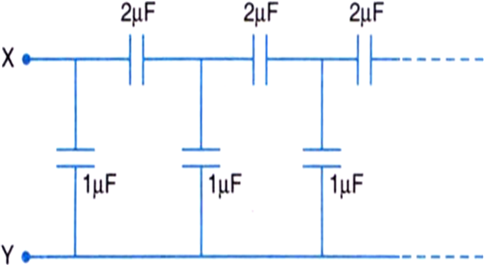 .
.
Textbook problems from chapter 3:
3.3 (page 119), 3.1 (page 118), 3.4 (page 119).
Notes: for problem 3.1, first read textbook §3.1.4 carefully;
for problem 3.4, average the electric field as a vector.
Due February 15 (Thursday); solutions.
Set 5
First, 4 textbook problems from chapter 3: 3.50 (page 164),
3.7 (page 129), 3.10 (page 130), 3.11 (page 130) [15 points].
Second, a reading assignment: textbook §3.2.4 (pages 127–129)
about image charges from spherical surfaces.
Note: I shall not explain this material in class.
Third, 2 more textbook problems from chapter 3 —
3.8 and 3.9 (both on page 129) — and a non-textbook problem:
- Work out the image charge method for a point charge located inside
a grounded conducting spherical shell.
(a) If the charge Q' is at distance b<R from the center,
where is the image charge and what is its value?
(b) Is there a net force on the point charge? If yes, find its magnitude and direction.
(c) What happens if the conducting spherical shell is not grounded?
[15 points]
Finally, 3 more textbook problems from chapter 3:
3.13, 3.14, and 3.15 (all on page 140).
Due February 22 (Thursday); solutions.
Set 6
Updated 2/28 at 3:35 PM
First, 6 textbook problems from chapter 3:
3.17 (page 149), 3.19 (page 149), 3.25 (page 150), 3.26 (page 150) [12 points],
3.43 (page 162) [18 points], and 3.55 (page 166) [18 points].
Second, a non-textbook problem:
A thin spherical shell of radius R has a non-uniform charge density σ(θ,φ),
but there are no charges outside on inside this shell.
Inside the sphere, the potential is V(x,y,z)=kxyz for some constant k.
(a) Rewrite this potential in spherical coordinates and expand it into a sum of terms of the form
(const)×rℓ×Yℓ,m(θ,φ).
For your convenience, here is a
table of spherical harmonics.
(b) Find the potential outside the spherical shell.
(c) Find the surface charge density σ(θ,φ) of the spherical shell.
Due March 5 (Tuesday); solutions.
Set 7
First, a few simple problems about electric dipoles:
3 textbook problems 3.29 (page 156), 3.30 (page 156), 3.53 (page 165) from chapter 3,
and a non-textbook problem:
The Northern hemisphere of a solid ball of radius R has uniform charge density +ρ0
while the Southern hemisphere has uniform density −ρ0.
Find the dipole moment of this ball and the potential it generates far away from the ball.
Second, 6 harder textbook problems (from chapters 3 and 4) about forces and torques on, by, and between electric dipoles:
3.57 (page 166) [12 points],
4.4 (page 170), 4.5 (page 171), 4.29 (page 205),
4.6 (page 172) [15 points], and 4.30 (page 205).
Note for problem 3.27: Assume the orbit is parallel to the xy plane and is centered somewhere
on the z axis.
Finally, 2 textbook problems from chapter 3 about electric quadrupoles and other multipoles:
3.46 (page 163), 3.27 (page 154).
Due March 19 (Tuesday); solutions.
Set 8
All problems in this set are from textbook chapter 4, and there are no non-textbook problems.
First, 4 problems about bound charges, E and D fields, and boundary conditions:
4.10 (page 176), 4.13 (page 179) [15 points],
4.15 (page 183), 4.16 (pages 183–4) [15 points].
Second, 2 problems about linear dielectrics and capacitors:
4.41 (page 208), 4.19 (page 191).
Third, a reading assignment: textbook §4.4.2 and my notes,
both on boundary problems in linear dielectrics.
Make sure you follow all the examples in detail, including the examples not discussed in class.
Finally, 3 actual problems boundary problems in linear dielectrics:
4.36 (page 206–7), 4.37 (page 207) [15 points], 4.25 (page 197).
Due March 26 (Tuesday); solutions.
Set 9
First, 2 textbook problems and one non-textbook problem about electric energy and forces in dielectrics:
4.26 (page 202), 4.28 (page 204) [15 points], and
- Consider a small dielectric ball in a non-uniform but slowly varying external electric field
Eext(x,y,z).
(a) Show that the net force on the ball is F=C∇(E2ext)
for some field-independent constant C.
(b) Show that this constant depends on the ball's radius R and dielectric constant ε as
C=2πε0R3(ε-1)/(ε+2).
Hint: see my notes on a dielectric ball in external field
for the ball's induced dipole moment.
Second, 2 reading assignments:
Note: I will not have time to discuss this material in class, so please read it on your own.
Third, a textbook problem and a non-textbook problem about charged particles moving in
combined E and B fields:
5.3 (page 216), and
- Consider the cycloid motion of a particle from the textbook example 5.2.
(a) Write down the net kinetic+potential energy of the particle.
(b) Verify that this net enegy is conserved in the cycloid motion.
Finally, 2 textbook problems about magnetic forces and electric currents:
5.4 (page 222), 5.10 (page 228) [15 points].
Note: in problem 5.10, use textbook eq. (5.39) for the magnetic field and mind its non-uniformity!
Due April 2 (Tuesday); solutions.
Set 10
First, a non-textbook problem about steady currents:
- A conducting cylinder of radius R and height H carries
electric current of density
J(x,y,z)=k(xx̂+yŷ-2zẑ),
where k is a constant and the (x,y,z) coordinates are counted from the center
of the cylinder's bottom disk.
(a) Can this current be steady, i.e., time-independent?
(b) What is the net current flowing through the cylinder?
Through which surface does it flow into the cylinder and through which surface
does it flow out?
Second, 6 textbook problems about Biot–Savart–Laplace formula for the magnetic field:
5.9 (page 228) [12 points], 5.11 (page 229),
5.6 (page 223) [8 points] and 5.12 (page 229) [12 points],
5.36 (page 255) [12 points], 5.50 (page 259)[12 points].
Note for problem 5.36: use eq. (5.89) for the magnetic dipole field.
Finally, 6 more textbook problems about Ampere Law and about the vector potential A:
5.16 (page 240), 5.18 (page 240), 5.24 (page 248),
5.25 (page 248), 5.26 (page 248), 5.30 (page 249).
Due April 9 (Tuesday); solutions.
Set 11
Reading assignments:
- Browse through Dr. Rudolf Winter's (Aberystwyth University, Wales, UK) notes on the origins
of diamagnetism, paramagnetism, and ferromagnetism, but skip the quantum details beyond the scope of this class:
- Read my notes «How to tell diamagnetic materials from paramagnetic».
- Read textbook §6.4.2 on saturation, hysteresis, and other non-linear effect in ferromagnetic materials.
Also, browse the wikipedia articles on ferromagnetism
and on magnetic domains.
Textbook problems from chapters 5 and 6:
5.58 (page 263),
6.8 (page 276), 6.10 (page 277), 6.12 (page 282), 6.13 (page 282),
6.20 (page 291).
Update: textbook problem 6.20 is removed from this set.
No non-textbook problems in this set.
Reading assignments due April 16 (Tuesday);
textbook problems due April 18 (Thursday); solutions.
Set 12
First, two textbook problems about electric power and EMF:
7.2 (page 302) and 7.5 (page 305).
Second, six textbook problems about Faraday Law of Induction and related issues:
7.7 (page 310–311), 7.8 (page 311), 7.12 (page 316), 7.17 (page 320–321),
7.19 (page 321) [15 points], 7.51 (page 348) [15 points].
Finally, three textbook problems about inductance and magnetic energy:
7.22 (page 327), 7.29 (page 331), 7.31 (page 331–332).
No non-textbook problems in this set.
Due April 25 (Thursday); solutions.
Exams
Last Modified: May 5, 2024.
Vadim Kaplunovsky
vadim@physics.utexas.edu
 .
.